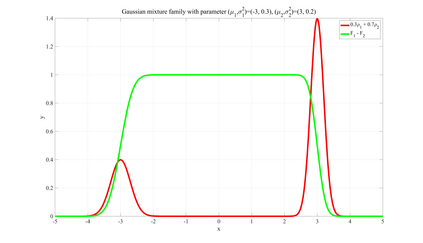
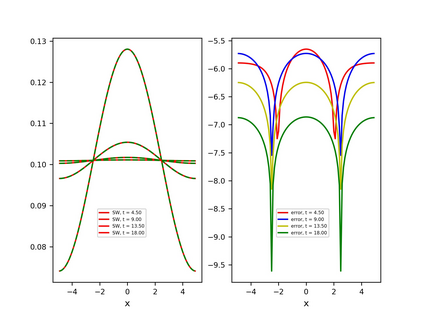
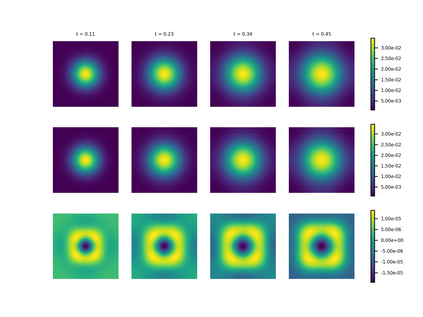
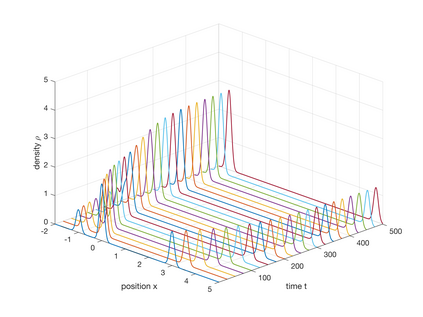
We consider the Wasserstein metric on the Gaussian mixture models (GMMs), which is defined as the pullback of the full Wasserstein metric on the space of smooth probability distributions with finite second moment. It derives a class of Wasserstein metrics on probability simplices over one-dimensional bounded homogeneous lattices via a scaling limit of the Wasserstein metric on GMMs. Specifically, for a sequence of GMMs whose variances tend to zero, we prove that the limit of the Wasserstein metric exists after certain renormalization. Generalizations of this metric in general GMMs are established, including inhomogeneous lattice models whose lattice gaps are not the same, extended GMMs whose mean parameters of Gaussian components can also change, and the second-order metric containing high-order information of the scaling limit. We further study the Wasserstein gradient flows on GMMs for three typical functionals: potential, internal, and interaction energies. Numerical examples demonstrate the effectiveness of the proposed GMM models for approximating Wasserstein gradient flows.
翻译:暂无翻译