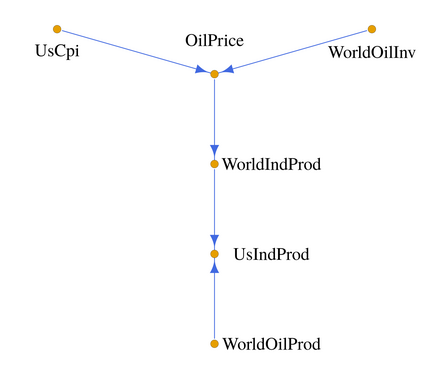
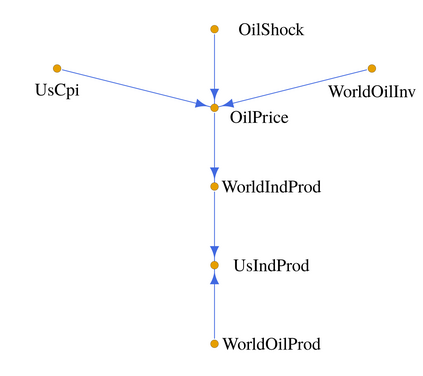
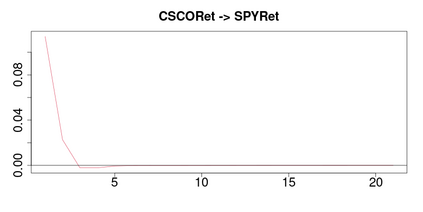
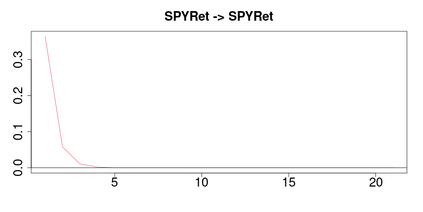
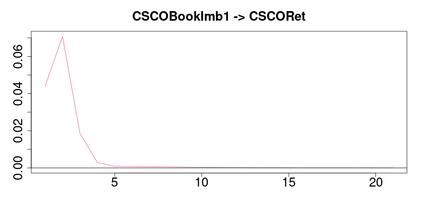
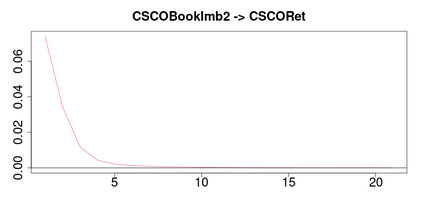
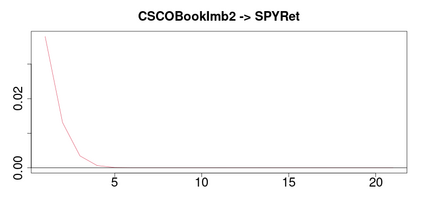
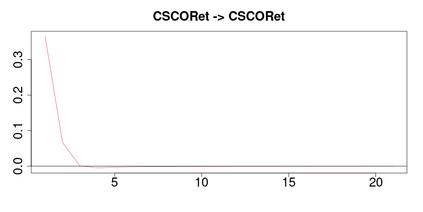
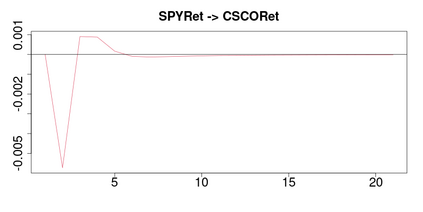
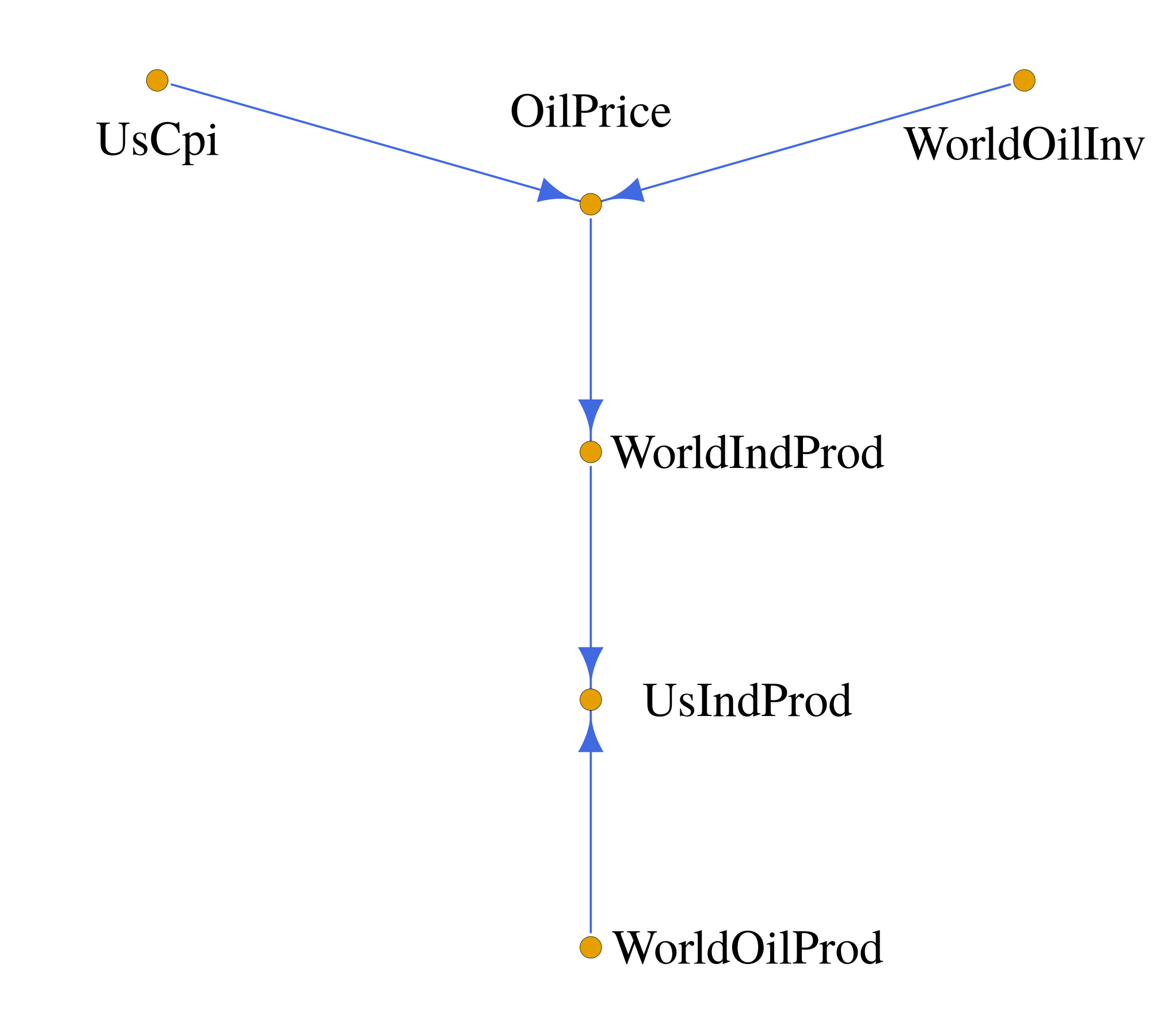
A methodology for high dimensional causal inference in a time series context is introduced. It is assumed that there is a monotonic transformation of the data such that the dynamics of the transformed variables are described by a Gaussian vector autoregressive process. This is tantamount to assume that the dynamics are captured by a Gaussian copula. No knowledge or estimation of the marginal distribution of the data is required. The procedure consistently identifies the parameters that describe the dynamics of the process and the conditional causal relations among the possibly high dimensional variables under sparsity conditions. The methodology allows us to identify such causal relations in the form of a directed acyclic graph. As illustrative applications we consider the impact of supply side oil shocks on the economy, and the causal relations between aggregated variables constructed from the limit order book on four stock constituents of the S&P500.
翻译:暂无翻译