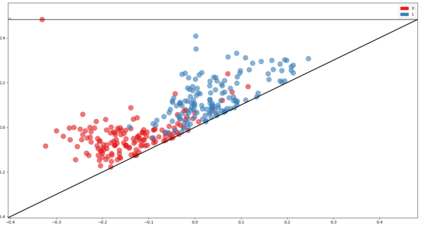
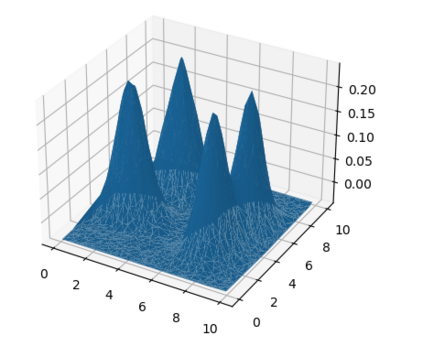
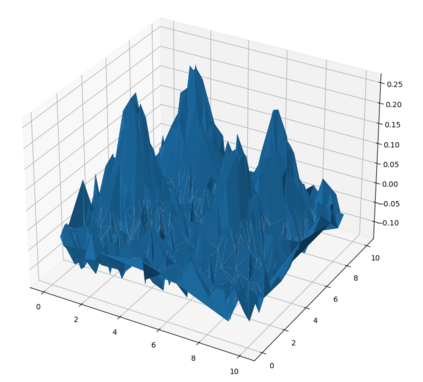
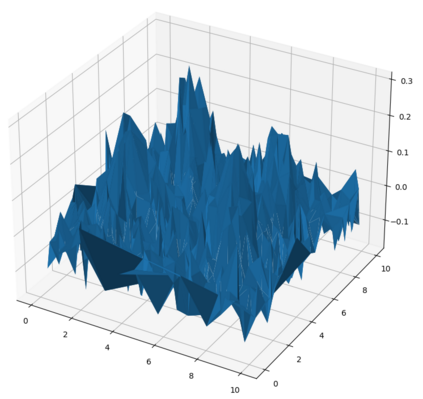
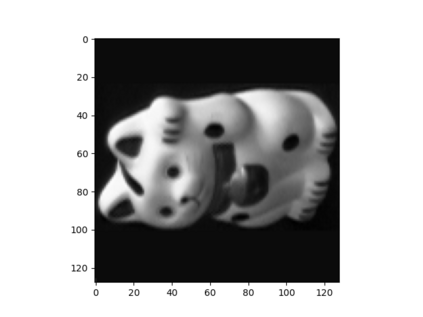
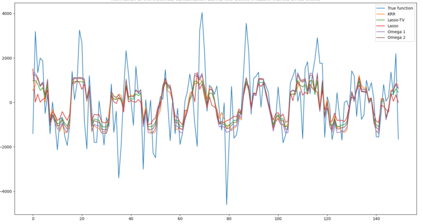
We study a regression problem on a compact manifold M. In order to take advantage of the underlying geometry and topology of the data, the regression task is performed on the basis of the first several eigenfunctions of the Laplace-Beltrami operator of the manifold, that are regularized with topological penalties. The proposed penalties are based on the topology of the sub-level sets of either the eigenfunctions or the estimated function. The overall approach is shown to yield promising and competitive performance on various applications to both synthetic and real data sets. We also provide theoretical guarantees on the regression function estimates, on both its prediction error and its smoothness (in a topological sense). Taken together, these results support the relevance of our approach in the case where the targeted function is ''topologically smooth''.
翻译:为了利用数据的基本几何学和地貌学,回归任务以该多元体Laplace-Beltrami操作员的最初几个元件为基础进行,这些元件有固定的示意性处罚。拟议处罚基于该元件或估计函数的子层层的地形学。总体方法显示在合成和真实数据集的各种应用中产生有希望和有竞争力的性能。我们还提供了关于回归函数估计数的理论保证,包括预测误差和平稳性(从表面学意义上讲)。这些结果加在一起,支持了我们的方法在目标函数为“结构上平稳”的情况下的相关性。