Tensor networks for unsupervised machine learning

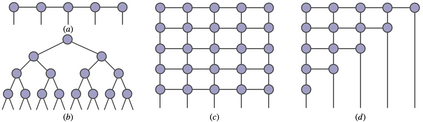
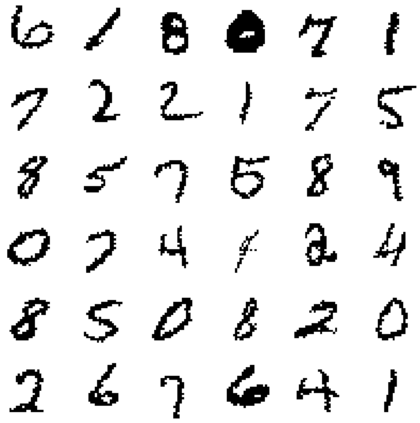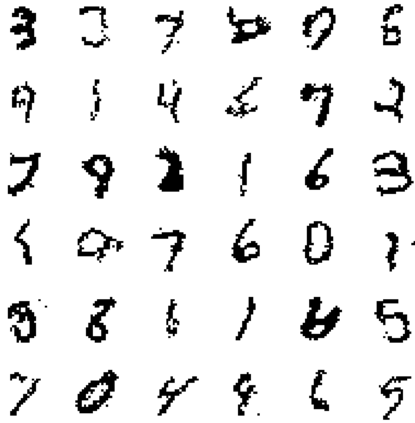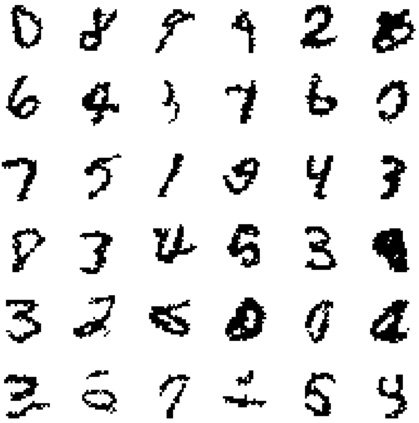Modeling the joint distribution of high-dimensional data is a central task in unsupervised machine learning. In recent years, many interests have been attracted to developing learning models based on tensor networks, which have advantages of theoretical understandings of the expressive power using entanglement properties, and as a bridge connecting the classical computation and the quantum computation. Despite the great potential, however, existing tensor-network-based unsupervised models only work as a proof of principle, as their performances are much worse than the standard models such as the restricted Boltzmann machines and neural networks. In this work, we present the Autoregressive Matrix Product States (AMPS), a tensor-network-based model combining the matrix product states from quantum many-body physics and the autoregressive models from machine learning. The model enjoys exact calculation of normalized probability and unbiased sampling, as well as a clear theoretical understanding of expressive power. We demonstrate the performance of our model using two applications, the generative modeling on synthetic and real-world data, and the reinforcement learning in statistical physics. Using extensive numerical experiments, we show that the proposed model significantly outperforms the existing tensor-network-based models and the restricted Boltzmann machines, and is competitive with the state-of-the-art neural network models.