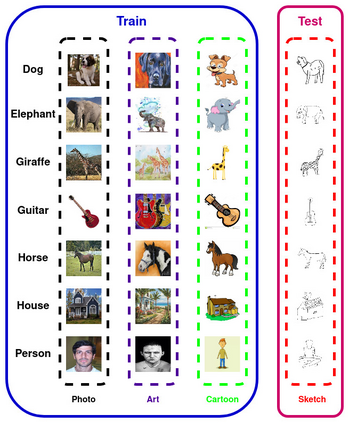
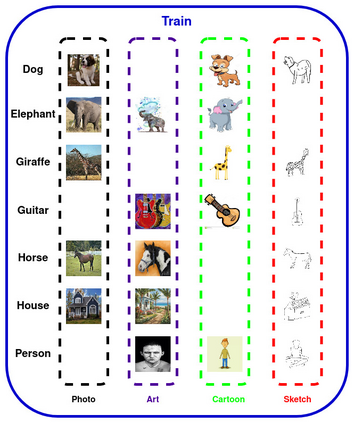
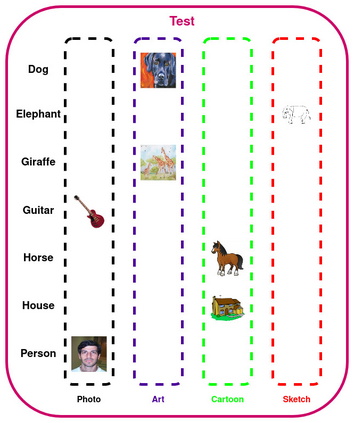
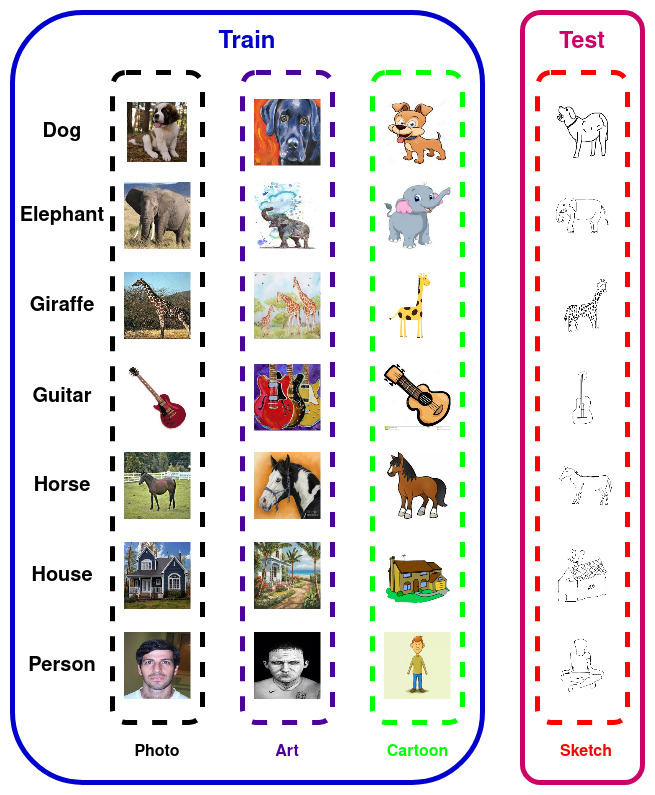
Domain generalization (DG) of machine learning algorithms is defined as their ability to learn a domain agnostic hypothesis from multiple training distributions, which generalizes onto data from an unseen domain. DG is vital in scenarios where the target domain with distinct characteristics has sparse data for training. Aligning with recent work~\cite{gulrajani2020search}, we find that a straightforward Empirical Risk Minimization (ERM) baseline consistently outperforms existing DG methods. We present ablation studies indicating that the choice of backbone, data augmentation, and optimization algorithms overshadows the many tricks and trades explored in the prior art. Our work leads to a new state of the art on the four popular DG datasets, surpassing previous methods by large margins. Furthermore, as a key contribution, we propose a classwise-DG formulation, where for each class, we randomly select one of the domains and keep it aside for testing. We argue that this benchmarking is closer to human learning and relevant in real-world scenarios. We comprehensively benchmark classwise-DG on the DomainBed and propose a method combining ERM and reverse gradients to achieve the state-of-the-art results. To our surprise, despite being exposed to all domains during training, the classwise DG is more challenging than traditional DG evaluation and motivates more fundamental rethinking on the problem of DG.
翻译:机器学习算法的广域化( DG) 的定义是,它们能够从多种培训分布中学习一个领域不可知的假设,这种假设可以概括到从无形领域获得的数据。 DG对于具有不同特点的目标领域缺乏培训数据的情况至关重要。我们发现,与最近的“cite{gulrajani2020Search}”工作相对照,一个直接的“经验风险最小化(ERM)”基线始终优于现有的DG方法。我们提出“激励”研究,表明主干、数据增强和优化算法的选择掩盖了在先前艺术中探索的许多花招和交易。我们的工作导致在四种流行的DG数据集上出现新的艺术状态,大大超越了先前的方法。此外,作为一个关键的贡献,我们提出了一种等级化的DG公式,我们在那里随机地选择一个领域,将它保留在测试中。我们的论点是,这一基准更接近人类学习,在现实世界情景中具有相关性。我们综合地将DG在DomaineB上对许多技巧和交易进行基准化,并提出了一种方法,在四种流行的DG数据集中比在进行更具有挑战性的DDDG的升级,在进行更接近于所有的升级的风险评估和反向风险的DDG中实现。