A Projection Algorithm for the Unitary Weights

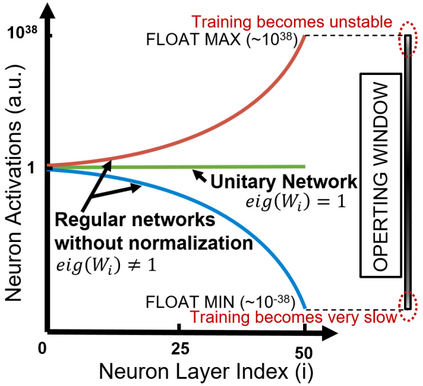
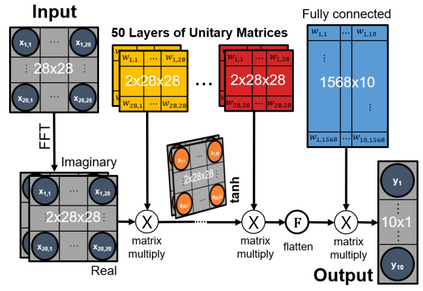
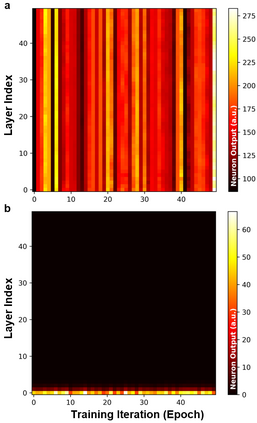
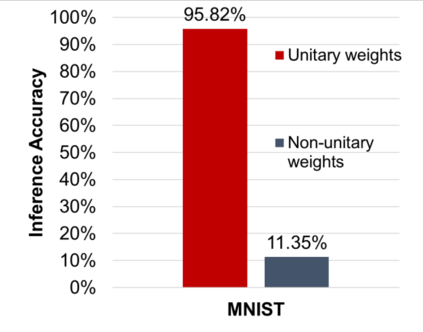
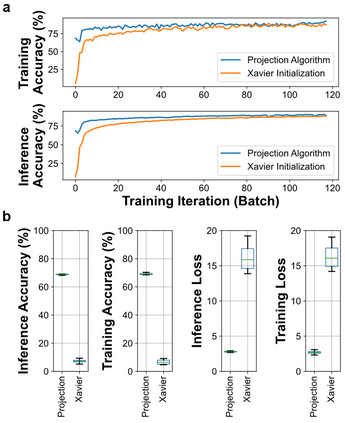
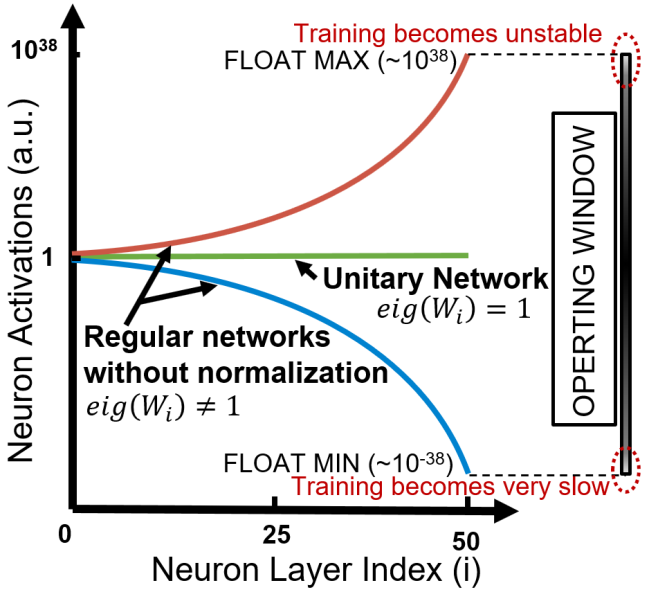
Unitary neural networks are promising alternatives for solving the exploding and vanishing activation/gradient problem without the need for explicit normalization that reduces the inference speed. However, they often require longer training time due to the additional unitary constraints on their weight matrices. Here we show a novel algorithm using a backpropagation technique with Lie algebra for computing approximated unitary weights from their pre-trained, non-unitary counterparts. The unitary networks initialized with these approximations can reach the desired accuracies much faster, mitigating their training time penalties while maintaining inference speedups. Our approach will be instrumental in the adaptation of unitary networks, especially for those neural architectures where pre-trained weights are freely available.