Fast compression of MCMC output

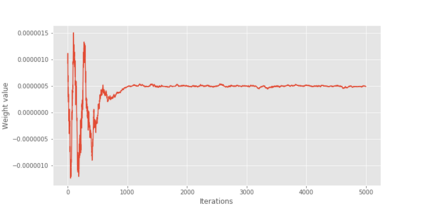
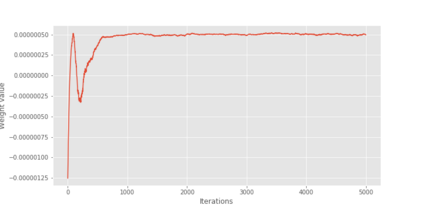
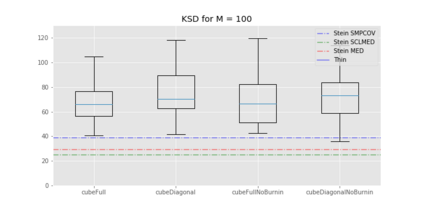
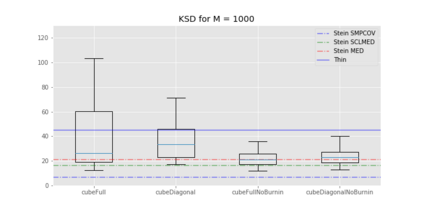
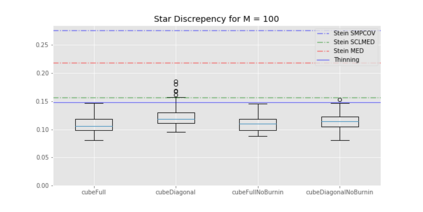
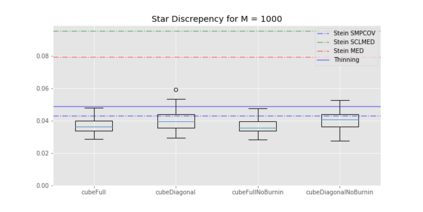
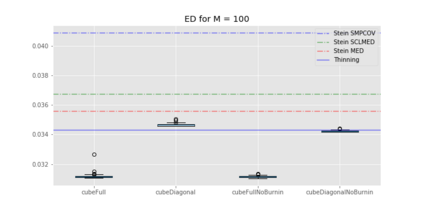
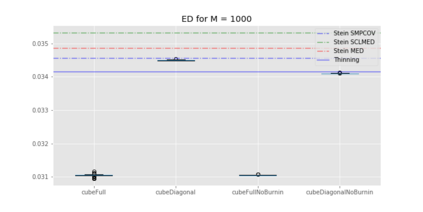
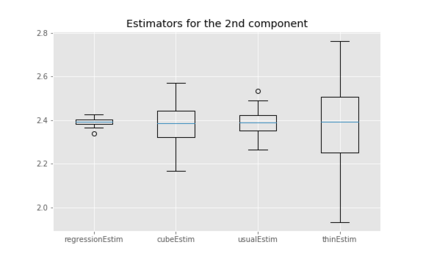
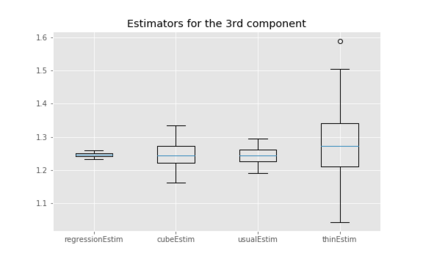
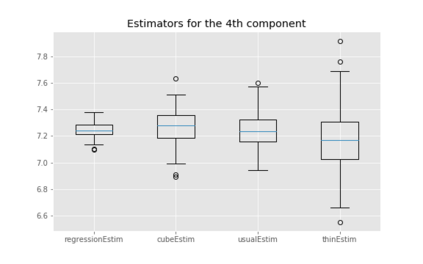
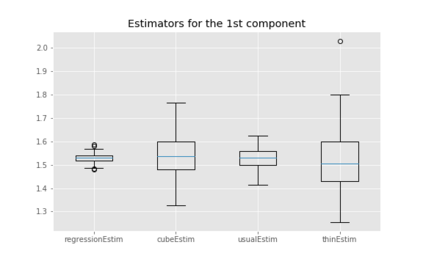
We propose cube thinning, a novel method for compressing the output of a MCMC (Markov chain Monte Carlo) algorithm when control variates are available. It amounts to resampling the initial MCMC sample (according to weights derived from control variates), while imposing equality constraints on averages of these control variates, using the cube method of [1]. Its main advantage is that its CPU cost is linear in N, the original sample size, and is constant in M, the required size for the compressed sample. This compares favourably to Stein thinning [2], which has complexity OpNM2q, and which requires the availability of the gradient of the target log-density (which automatically implies the availability of control variates). Our numerical experiments suggest that cube thinning is also competitive in terms of statistical error.