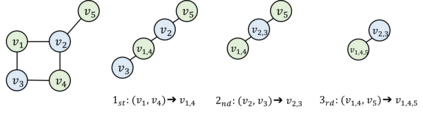
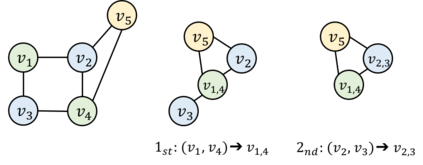
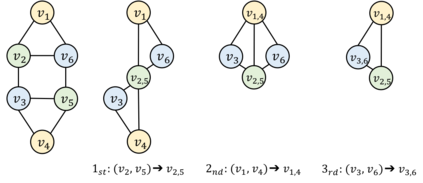
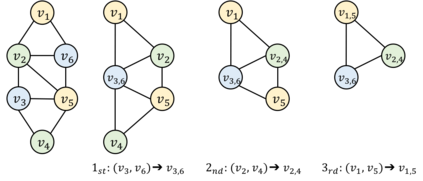
In this paper, we consider the topological interference management (TIM) problem in a dynamic setting, where an adversary perturbs network topology to prevent the exploitation of sophisticated coding opportunities (e.g., interference alignment). Focusing on a special class of network topology - chordal networks - we investigate algorithmic aspects of the TIM problem under adversarial topology perturbation. In particular, given the adversarial perturbation with respect to edge insertion/deletion, we propose a dynamic graph coloring algorithm that allows for a constant number of re-coloring updates against each inserted/deleted edge to achieve the information-theoretic optimality. This is a sharp reduction of the general graph re-coloring, whose optimal number of updates scales as the size of the network, thanks to the delicate exploitation of the structural properties of weakly chordal graphs.
翻译:在本文中,我们考虑在动态环境中的地形干扰管理(TIM)问题,在动态环境中,敌手扰动网络地形学可以防止利用复杂的编码机会(例如干扰校正),集中关注特殊类别的网络地形学(chordal网络),在对抗性地形扰动下,我们调查TIM问题的算法方面。特别是,鉴于边缘插入/删除方面的对抗性扰动,我们提议一种动态图表色谱算法,允许对每个插入/删除的边缘不断进行多次重新彩色更新,以达到信息理论的最佳性。这是对一般图的重新色化的急剧缩小,由于对微弱的色谱图的结构特性的微妙利用,一般图的重新色化规模与网络的大小相比是最佳的。