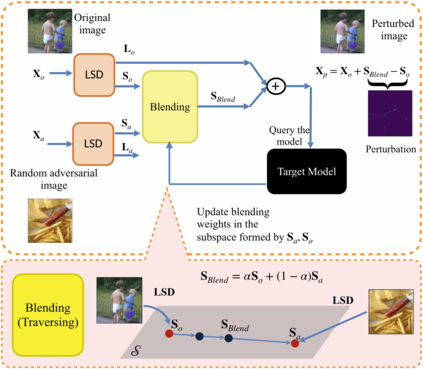
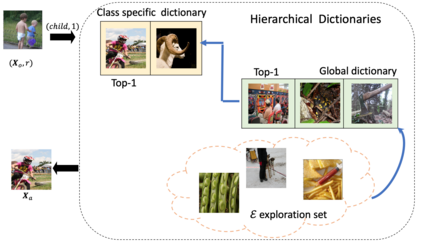
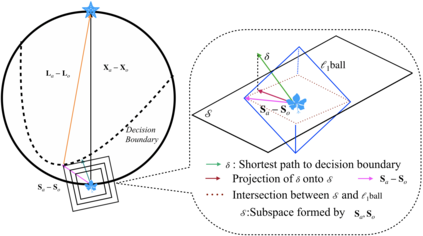
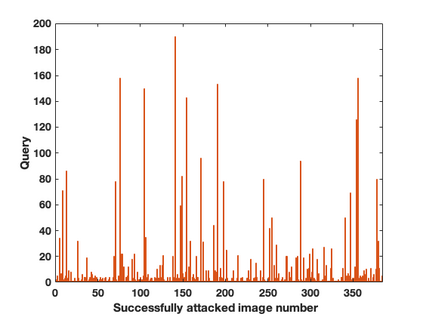
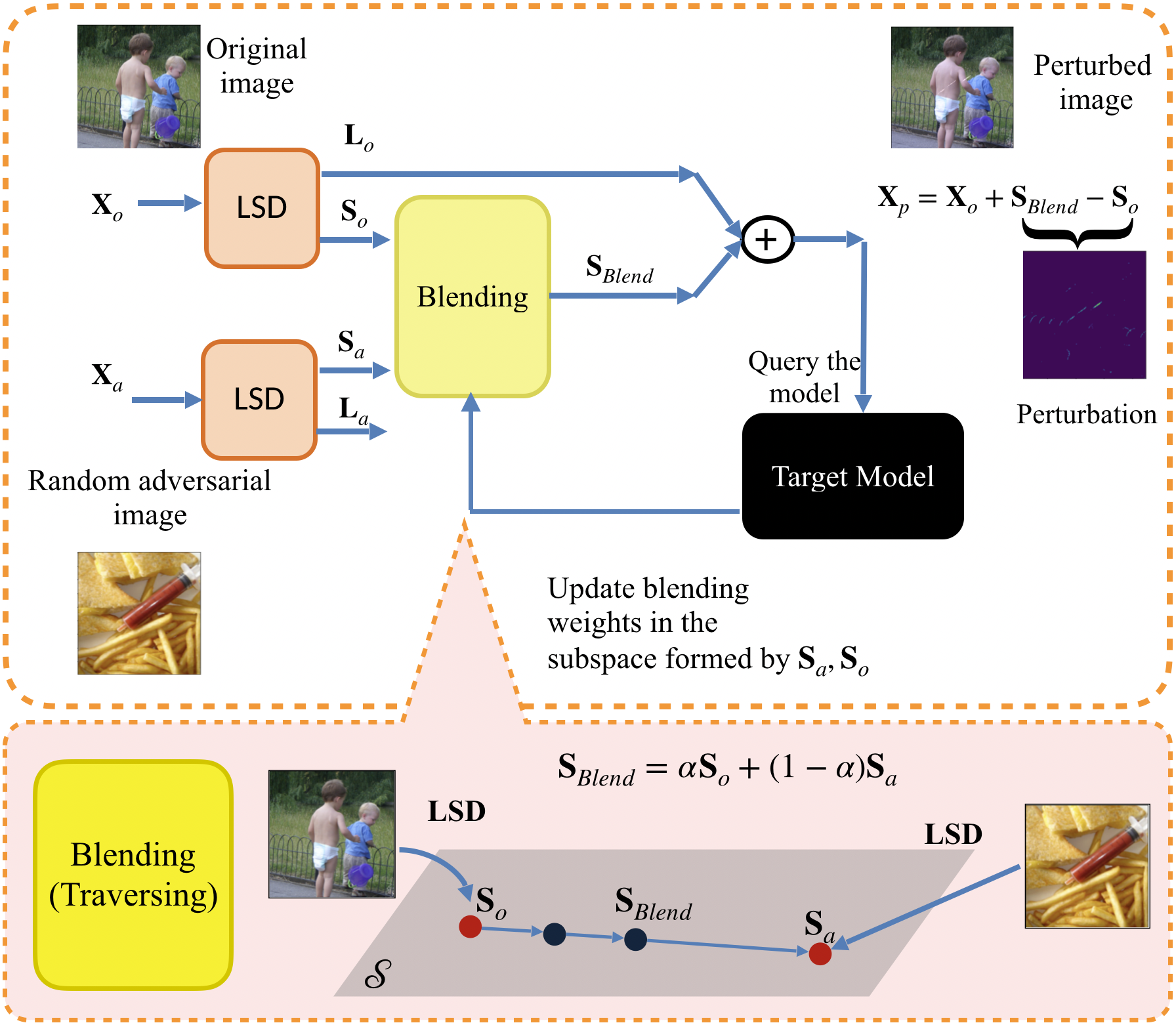
We propose LSDAT, an image-agnostic decision-based black-box attack that exploits low-rank and sparse decomposition (LSD) to dramatically reduce the number of queries and achieve superior fooling rates compared to the state-of-the-art decision-based methods under given imperceptibility constraints. LSDAT crafts perturbations in the low-dimensional subspace formed by the sparse component of the input sample and that of an adversarial sample to obtain query-efficiency. The specific perturbation of interest is obtained by traversing the path between the input and adversarial sparse components. It is set forth that the proposed sparse perturbation is the most aligned sparse perturbation with the shortest path from the input sample to the decision boundary for some initial adversarial sample (the best sparse approximation of shortest path, likely to fool the model). Theoretical analyses are provided to justify the functionality of LSDAT. Unlike other dimensionality reduction based techniques aimed at improving query efficiency (e.g, ones based on FFT), LSD works directly in the image pixel domain to guarantee that non-$\ell_2$ constraints, such as sparsity, are satisfied. LSD offers better control over the number of queries and provides computational efficiency as it performs sparse decomposition of the input and adversarial images only once to generate all queries. We demonstrate $\ell_0$, $\ell_2$ and $\ell_\infty$ bounded attacks with LSDAT to evince its efficiency compared to baseline decision-based attacks in diverse low-query budget scenarios as outlined in the experiments.
翻译:我们提议LSDAT, 这是一种基于图像的、不可知的基于决定的黑盒攻击, 利用低调和稀少的分解组件( LSD) 来大幅降低查询次数, 并实现比在不易感化的限制下采用最先进的基于决定的方法高的愚弄率。 LSDAT在由输入样本的稀疏成分和为获得查询效率而使用对立样本形成的低维子空间中, 手工艺在低维度子空间中进行扰动。 具体干扰利益的方法是通过在输入和敌对稀薄的稀薄组件之间穿行走基底线。 它规定, 提议的稀薄的扰动是最松动的弯曲, 与从输入样本到决定边界的最短的路径相比, 最短的滑动率。 LSDT 与其他基于提高查询效率的技术不同( 例如基于FFFT), LSD直接在图像 Pixel 域中进行低基调的操作, 保证它比不值 =ell_ exalbreal exaltial decal decal decalation exation exation exationsaltiews) exation as the scaration exations as the saltiquedudududududustration.