Robust Learning via Persistency of Excitation

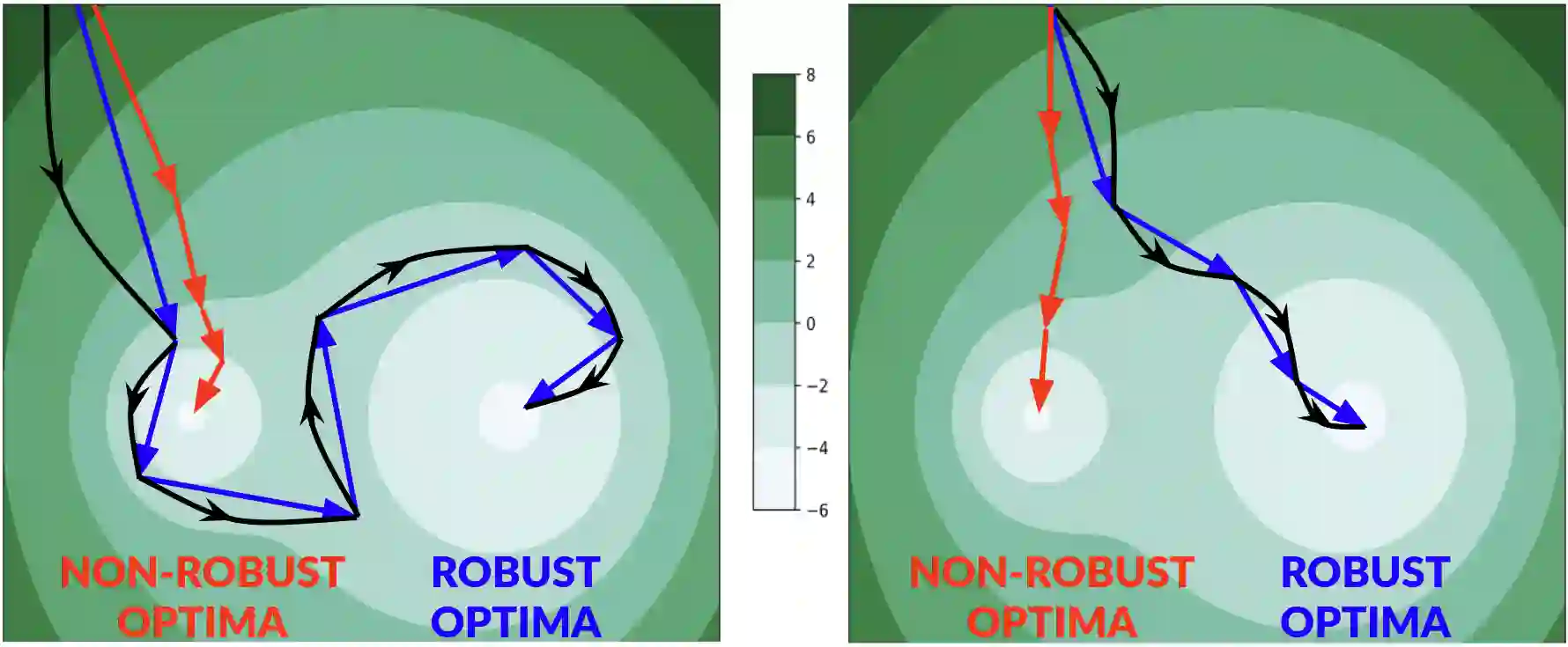
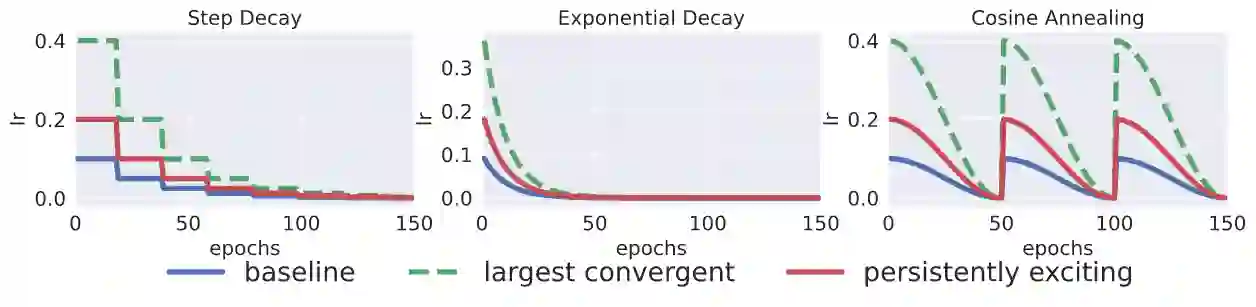
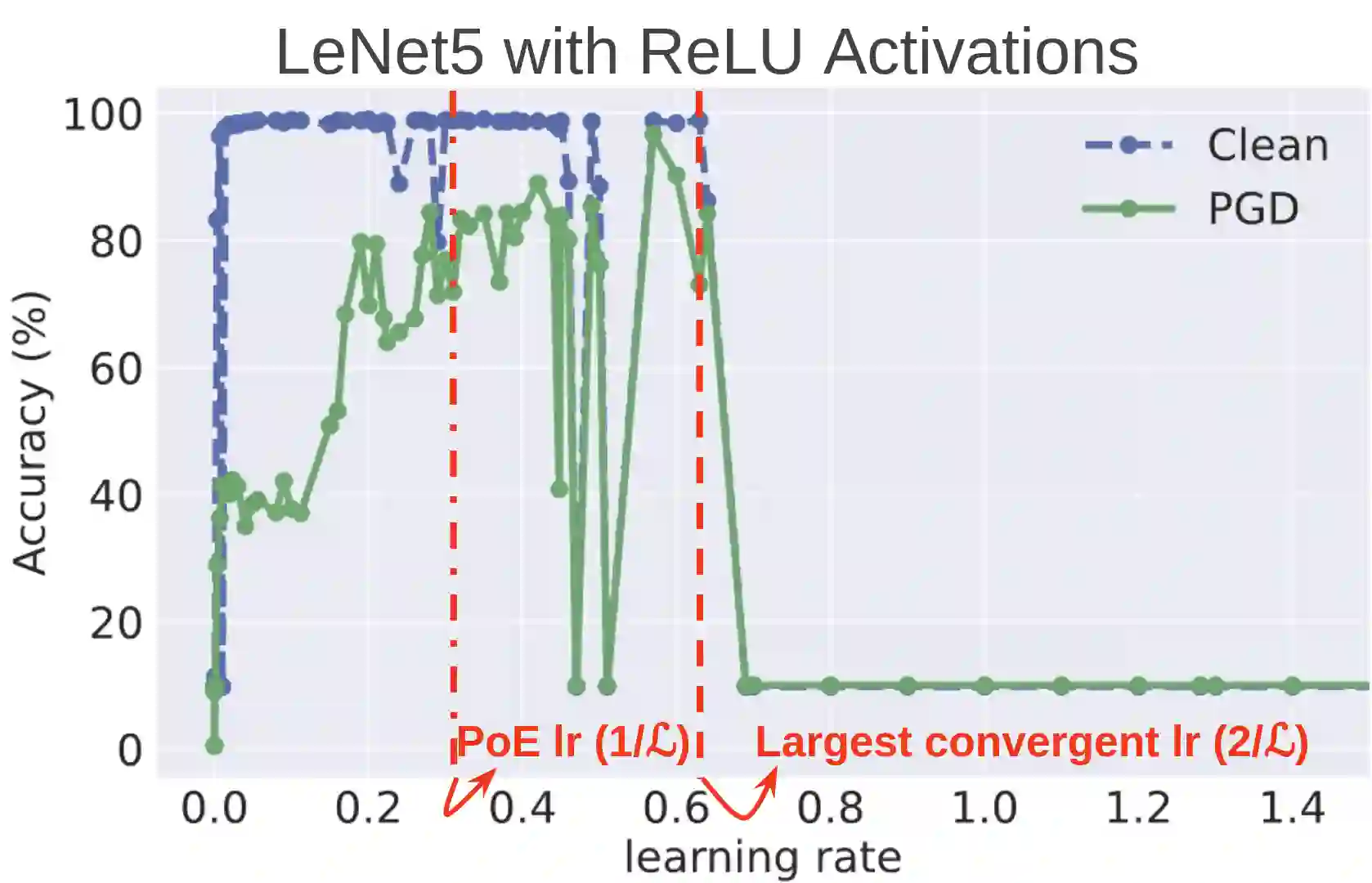
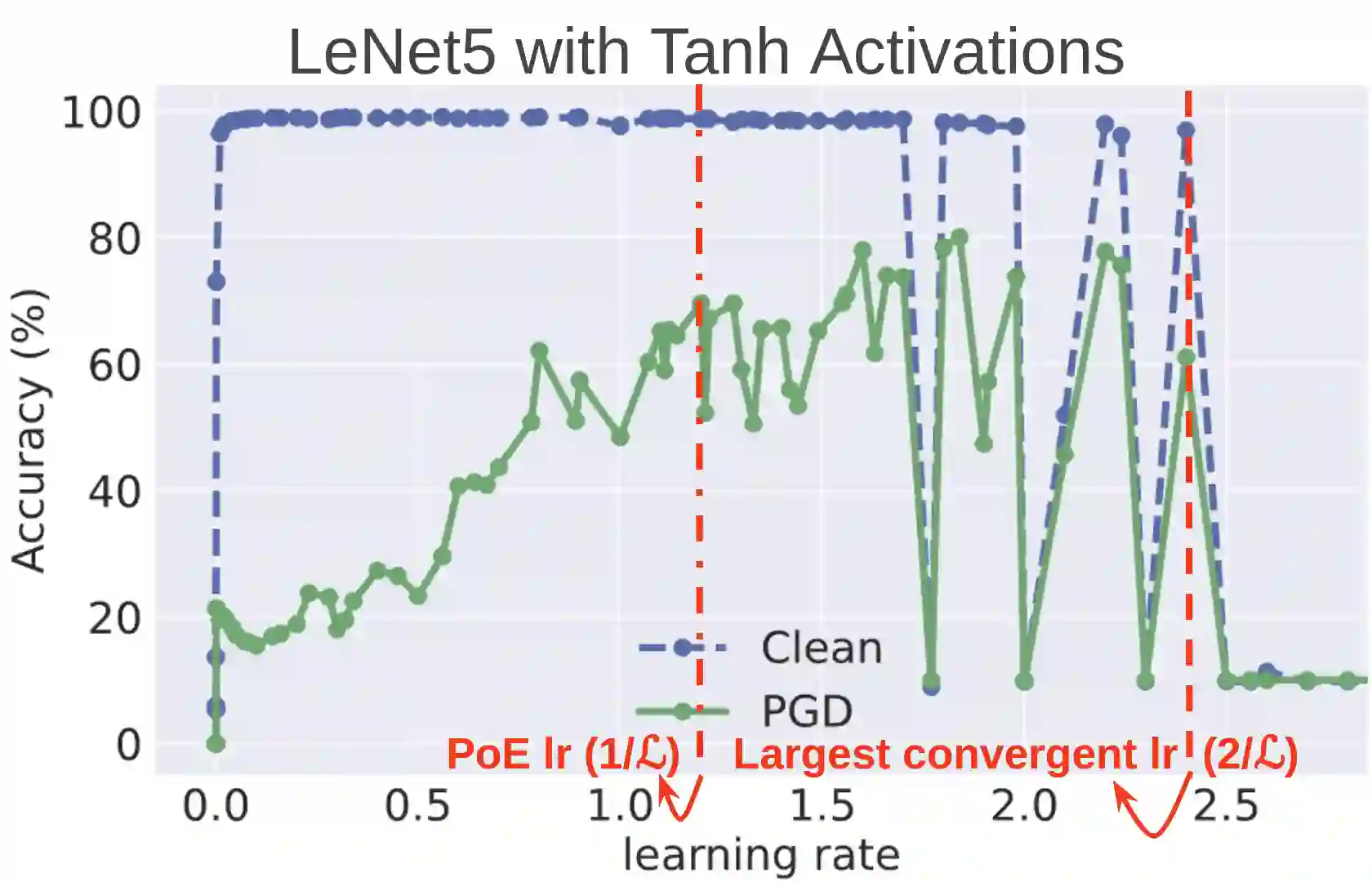
Improving adversarial robustness of neural networks remains a major challenge. Fundamentally, training a network is a parameter estimation problem. In adaptive control theory, maintaining persistency of excitation (PoE) is integral to ensuring convergence of parameter estimates in dynamical systems to their robust optima. In this work, we show that network training using gradient descent is equivalent to a dynamical system parameter estimation problem. Leveraging this relationship, we prove a sufficient condition for PoE of gradient descent is achieved when the learning rate is less than the inverse of the Lipschitz constant of the gradient of loss function. We provide an efficient technique for estimating the corresponding Lipschitz constant using extreme value theory and demonstrate that by only scaling the learning rate schedule we can increase adversarial accuracy by up to 15% points on benchmark datasets. Our approach also universally increases the adversarial accuracy by 0.1% to 0.3% points in various state-of-the-art adversarially trained models on the AutoAttack benchmark, where every small margin of improvement is significant.