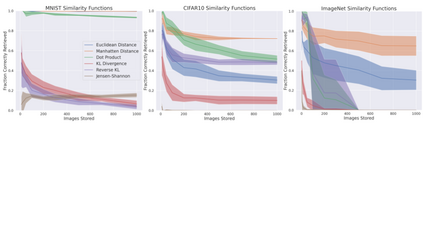
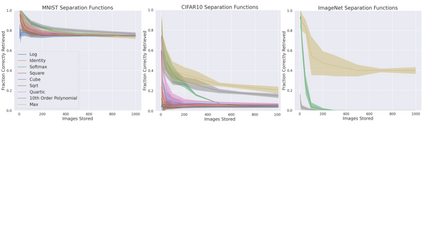
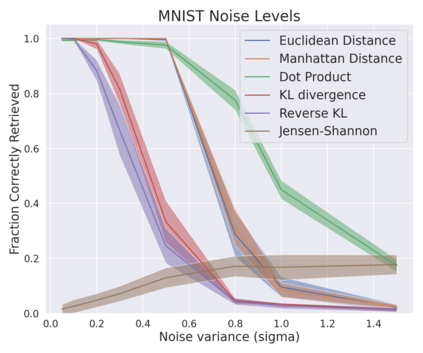
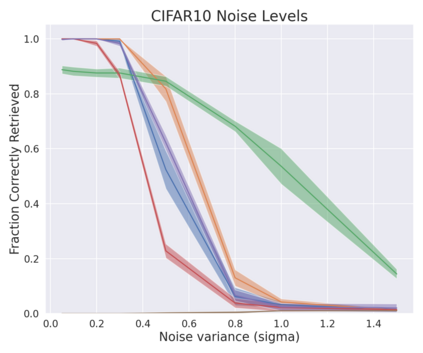
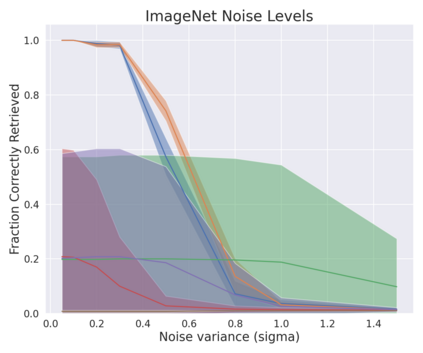
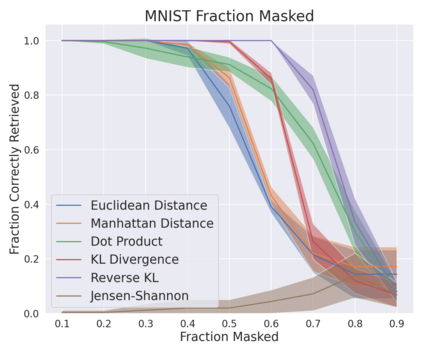
A large number of neural network models of associative memory have been proposed in the literature. These include the classical Hopfield networks (HNs), sparse distributed memories (SDMs), and more recently the modern continuous Hopfield networks (MCHNs), which possesses close links with self-attention in machine learning. In this paper, we propose a general framework for understanding the operation of such memory networks as a sequence of three operations: similarity, separation, and projection. We derive all these memory models as instances of our general framework with differing similarity and separation functions. We extend the mathematical framework of Krotov et al (2020) to express general associative memory models using neural network dynamics with only second-order interactions between neurons, and derive a general energy function that is a Lyapunov function of the dynamics. Finally, using our framework, we empirically investigate the capacity of using different similarity functions for these associative memory models, beyond the dot product similarity measure, and demonstrate empirically that Euclidean or Manhattan distance similarity metrics perform substantially better in practice on many tasks, enabling a more robust retrieval and higher memory capacity than existing models.
翻译:文献中提出了大量连接记忆的神经网络模型,其中包括古典Hopfield网络(HNs),分散的记忆(SDMs),以及最近的现代连续Hopfield网络(MCHNs),这些网络与机器学习中的自我意识有着密切的联系。在本文件中,我们提出了一个总体框架,用以理解这种记忆网络的运行,作为三种操作的序列:相似性、分离性和投影。我们从所有这些记忆模型中得出,作为我们总体框架的例子,具有不同的相似性和分离功能。我们扩展了Krotov等人(202020年)的数学框架,以表达使用神经人之间只有二级互动的神经网络动态的一般联系记忆模型,并形成一种一般的能量功能,这是该动态的Lyapunov函数。最后,我们利用我们的框架,对使用不同相似性功能进行实验性研究,这些连接记忆模型使用不同相似性功能的能力,超越了点产品相似性测量标准,并用经验证明Euclidean或曼哈哈顿距离指标在许多任务上表现得好得多,使得检索能力比现有模型更有力和更高的记忆能力。