Regularization for Shuffled Data Problems via Exponential Family Priors on the Permutation Group

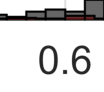
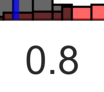
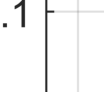
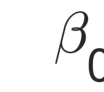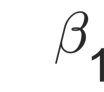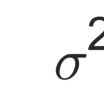In the analysis of data sets consisting of (X, Y)-pairs, a tacit assumption is that each pair corresponds to the same observation unit. If, however, such pairs are obtained via record linkage of two files, this assumption can be violated as a result of mismatch error rooting, for example, in the lack of reliable identifiers in the two files. Recently, there has been a surge of interest in this setting under the term "Shuffled data" in which the underlying correct pairing of (X, Y)-pairs is represented via an unknown index permutation. Explicit modeling of the permutation tends to be associated with substantial overfitting, prompting the need for suitable methods of regularization. In this paper, we propose a flexible exponential family prior on the permutation group for this purpose that can be used to integrate various structures such as sparse and locally constrained shuffling. This prior turns out to be conjugate for canonical shuffled data problems in which the likelihood conditional on a fixed permutation can be expressed as product over the corresponding (X,Y)-pairs. Inference is based on the EM algorithm in which the intractable E-step is approximated by the Fisher-Yates algorithm. The M-step is shown to admit a significant reduction from $n^2$ to $n$ terms if the likelihood of (X,Y)-pairs has exponential family form as in the case of generalized linear models. Comparisons on synthetic and real data show that the proposed approach compares favorably to competing methods.