Extensions of Random Orthogonal Matrix Simulation for Targetting Kollo Skewness

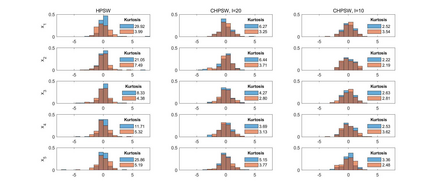
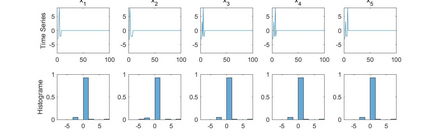
Modelling multivariate systems is important for many applications in engineering and operational research. The multivariate distributions under scrutiny usually have no analytic or closed form. Therefore their modelling employs a numerical technique, typically multivariate simulations, which can have very high dimensions. Random Orthogonal Matrix (ROM) simulation is a method that has gained some popularity because of the absence of certain simulation errors. Specifically, it exactly matches a target mean, covariance matrix and certain higher moments with every simulation. This paper extends the ROM simulation algorithm presented by Hanke et al. (2017), hereafter referred to as HPSW, which matches the target mean, covariance matrix and Kollo skewness vector exactly. Our first contribution is to establish necessary and sufficient conditions for the HPSW algorithm to work. Our second contribution is to develop a general approach for constructing admissible values in the HPSW. Our third theoretical contribution is to analyse the effect of multivariate sample concatenation on the target Kollo skewness. Finally, we illustrate the extensions we develop here using a simulation study.