Differentially private sparse vectors with low error, optimal space, and fast access

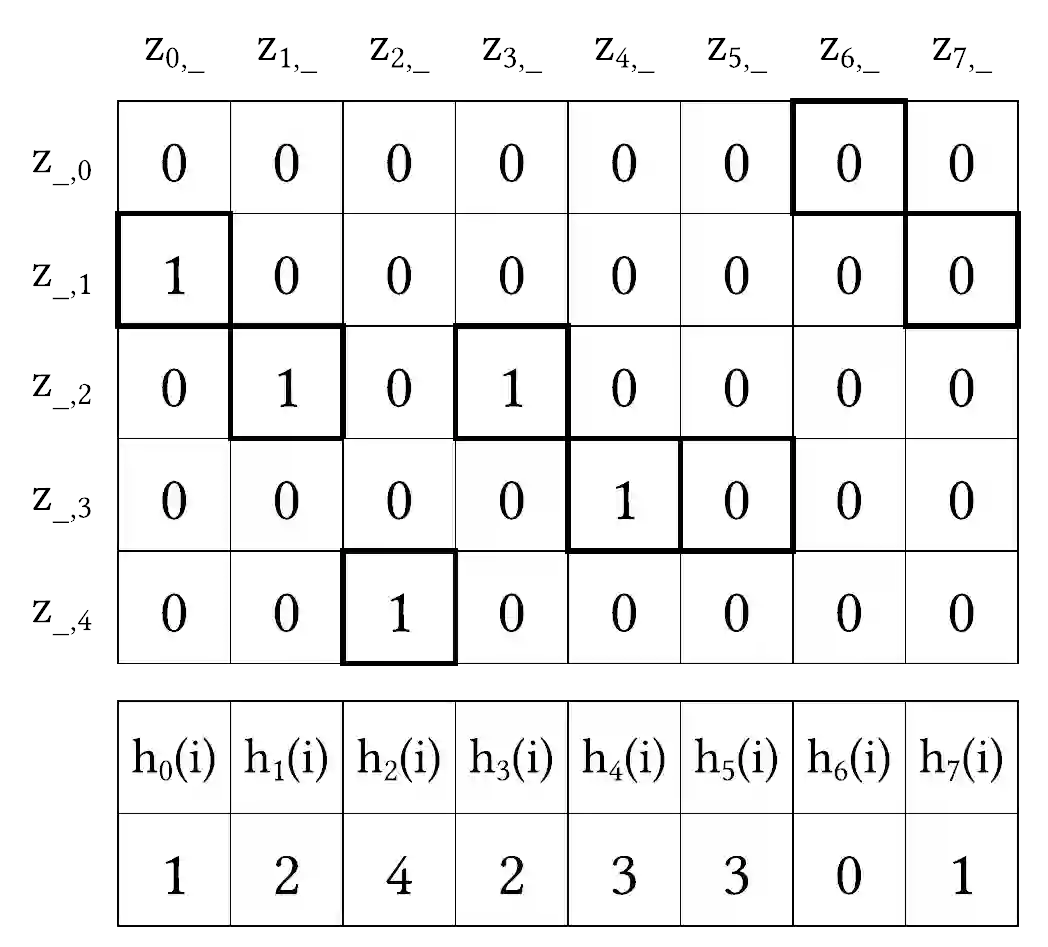
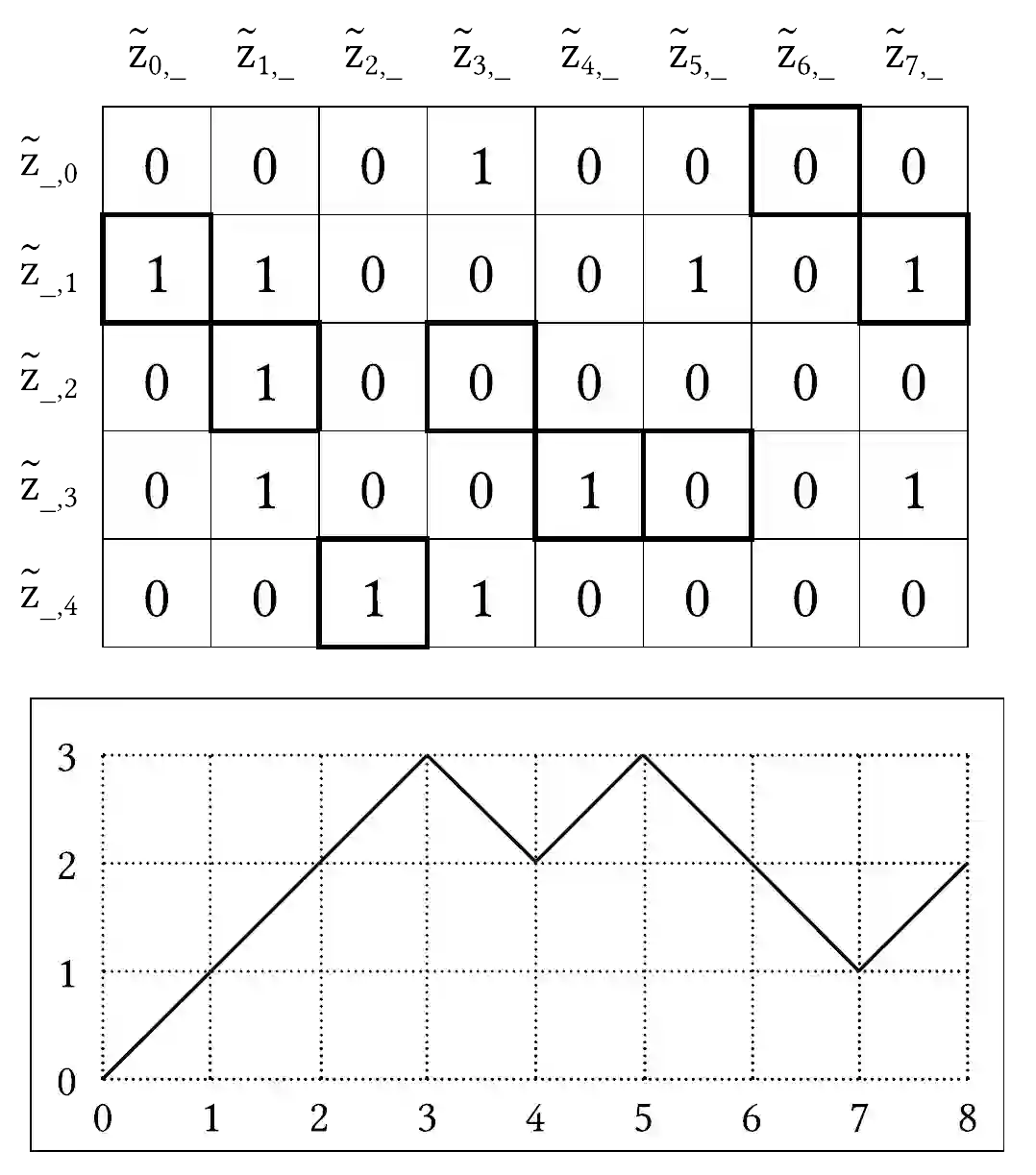
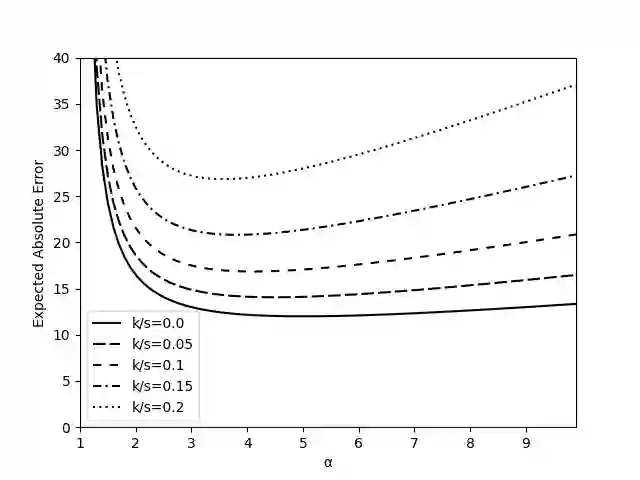
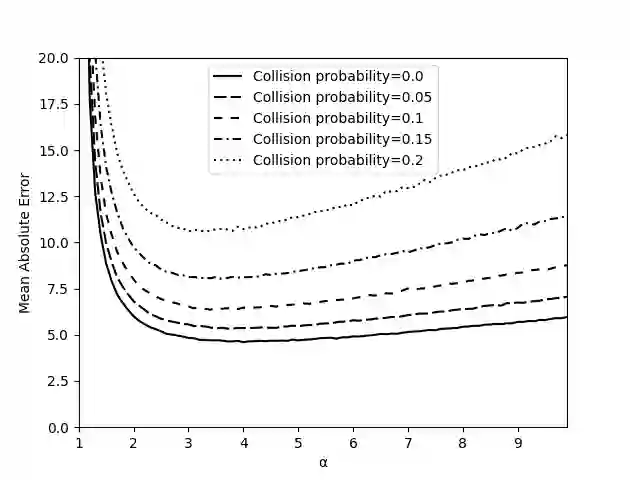
Representing a sparse histogram, or more generally a sparse vector, is a fundamental task in differential privacy. An ideal solution would use space close to information-theoretical lower bounds, have an error distribution that depends optimally on the desired privacy level, and allow fast random access to entries in the vector. However, existing approaches have only achieved two of these three goals. In this paper we introduce the Approximate Laplace Projection (ALP) mechanism for approximating k-sparse vectors. This mechanism is shown to simultaneously have information-theoretically optimal space (up to constant factors), fast access to vector entries, and error of the same magnitude as the Laplace-mechanism applied to dense vectors. A key new technique is a unary representation of small integers, which is shown to be robust against ``randomized response'' noise. This representation is combined with hashing, in the spirit of Bloom filters, to obtain a space-efficient, differentially private representation. Our theoretical performance bounds are complemented by simulations which show that the constant factors on the main performance parameters are quite small, suggesting practicality of the technique.