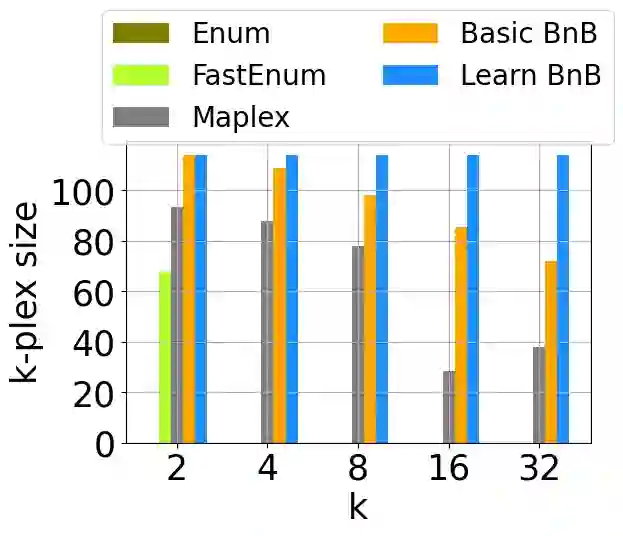
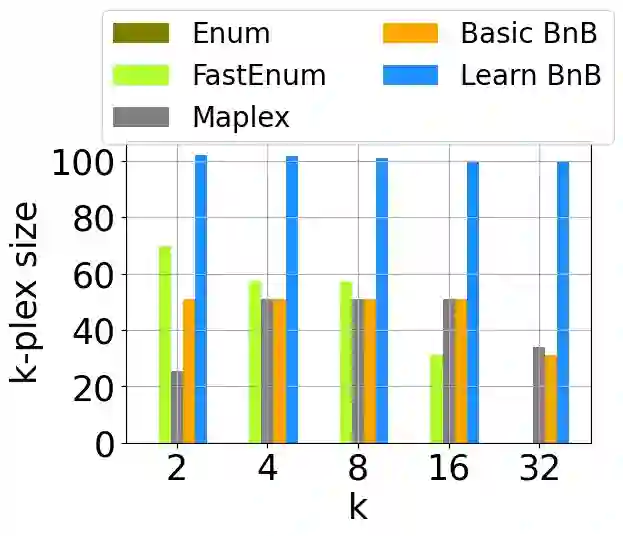
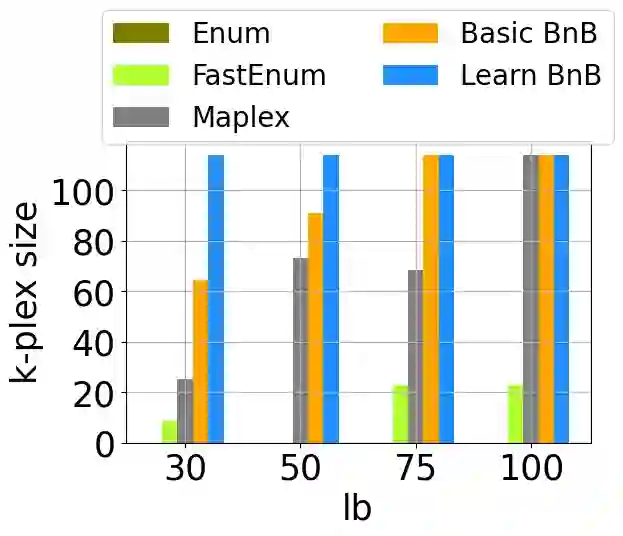
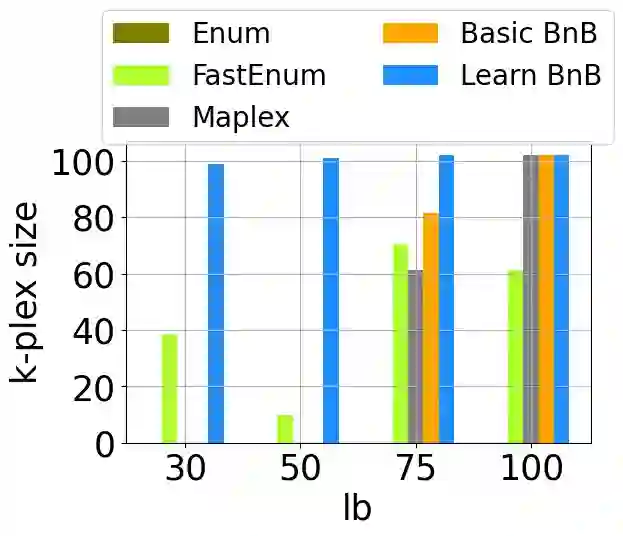
k-plex is a representative definition of communities in networks. While the cliques is too stiff to applicate to real cases, the k-plex relaxes the notion of the clique, allowing each node to miss up to k connections. Although k-plexes are more flexible than cliques, finding them is more challenging as their number is greater. In this paper, we aim to detect the k-plex under the size and time constraints, leveraging the new vision of automated learning bounding strategy. We introduce the constraint learning concept to learn the bound strategy from the branch and bound process and develop it into a Mixed Integer Programming framework. While most of the work is dedicated on learn the branch strategy in branch and bound-based algorithms, we focus on the learn to bound strategy which needs to handle the problem that learned strategy might not examine the feasible solution. We adopted the MILP framework and design a set of variables relative to the k-plex property as our constraint space to learn the strategy. The learn to bound strategy learning the original strategy function also reduces the computation load of the bound process to accelerate the branch and bound algorithm. Note that the learn to bound concept can apply to any branch and bound based algorithm with the appropriate framework. We conduct the experiment on different networks, the results show that our learn to branch and bound method does accelerate the original branch and bound method and outperforms other baselines, while also being able to generalize on different graph properties.
翻译:kplex 是一个具有代表性的网络社区定义。 虽然 clicques过于僵硬,无法与真实案例相适应, 但是 kplex 却放松了 clique 的概念, 允许每个节点错过 k 连接。 虽然 kplex 要比 cliques 更灵活, 发现它们更具有挑战性, 因为其数量更大。 在本文件中, 我们的目标是在规模和时间限制下检测 kplus, 利用自动学习约束战略的新愿景 。 我们引入了限制学习概念, 从分支学习约束战略, 并把它发展到混合 Interger 编程框架 。 虽然大多数工作都致力于在分支和基于约束的算法中学习分支战略, 但是我们侧重于学习约束战略, 解决那些需要解决的难题。 我们采用了 MILP 框架, 并设计一套与 klobal 属性相关的变量作为学习策略的制约空间 。 我们学习约束战略 学习原始战略功能还减少了绑定过程的计算负荷, 以加快分支和绑定的算法 。 注意, 绑定的网络可以约束性概念在约束性框架上, 学习任何分支 并显示任何约束性框架 并显示我们以合适的方法 。