Enhanced Multi-Objective A* Using Balanced Binary Search Trees

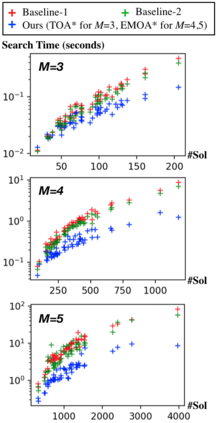
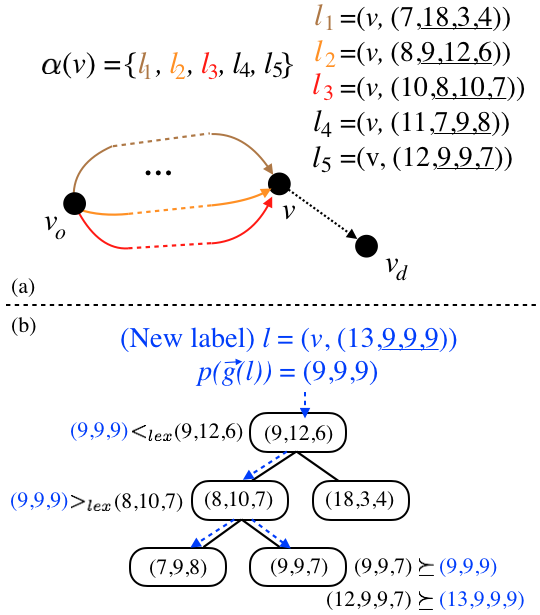
This work addresses the Multi-Objective Shortest Path Problem (MO-SPP): Given a graph where each edge is associated with a non-negative cost vector, MO-SPP aims to find all the Pareto-optimal paths connecting the given start and goal nodes. To solve MO-SPP, the popular multi-objective A* (MOA*) like algorithms maintain a "frontier" set at any node during the search to keep track of the non-dominated paths that reach that node. The computational efficiency of MOA* algorithms directly depend on how efficiently one can maintain the frontier sets. Recently, several techniques have been developed in the literature to address this issue mainly for two objectives. In this work, we introduce a new method to efficiently maintain these frontiers for multiple objectives by leveraging balanced binary search trees. We provide extensive simulation results for problems with three, four and five objectives to show that our method outperforms existing techniques by an order of magnitude in general.