Self-Supervised Training with Autoencoders for Visual Anomaly Detection

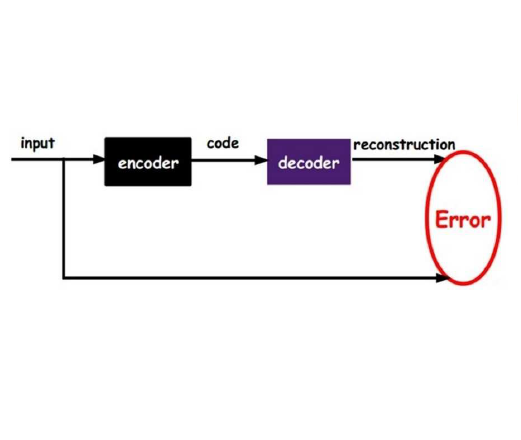
We focus on a specific use case in anomaly detection where the distribution of normal samples is supported by a lower-dimensional manifold. Here, regularized autoencoders provide a popular approach by learning the identity mapping on the set of normal examples, while trying to prevent good reconstruction on points outside of the manifold. Typically, this goal is implemented by controlling the capacity of the model, either directly by reducing the size of the bottleneck layer or implicitly by imposing some sparsity (or contraction) constraints on parts of the corresponding network. However, neither of these techniques does explicitly penalize the reconstruction of anomalous signals often resulting in poor detection. We tackle this problem by adapting a self-supervised learning regime that exploits discriminative information during training but focuses on the submanifold of normal examples. Informally, our training objective regularizes the model to produce locally consistent reconstructions, while replacing irregularities by acting as a filter that removes anomalous patterns. To support this intuition, we perform a rigorous formal analysis of the proposed method and provide a number of interesting insights. In particular, we show that the resulting model resembles a non-linear orthogonal projection of partially corrupted images onto the submanifold of uncorrupted samples. On the other hand, we identify the orthogonal projection as an optimal solution for a number of regularized autoencoders including the contractive and denoising variants. We support our theoretical analysis by empirical evaluation of the resulting detection and localization performance of the proposed method. In particular, we achieve a new state-of-the-art result on the MVTec AD dataset -- a challenging benchmark for visual anomaly detection in the manufacturing domain.