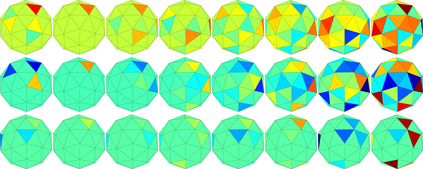
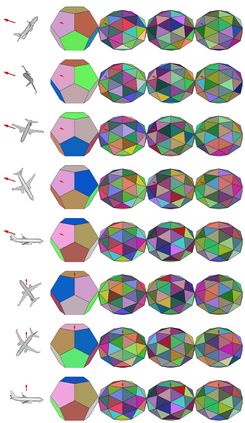
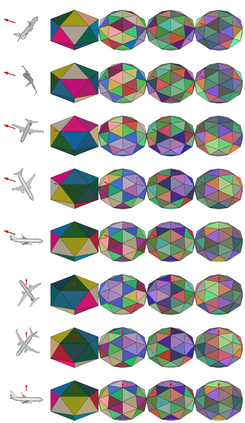
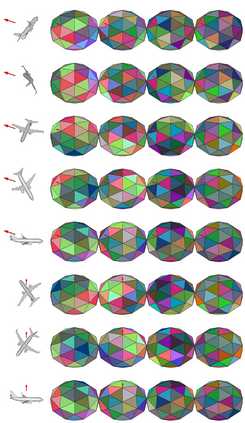
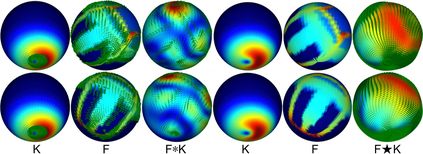
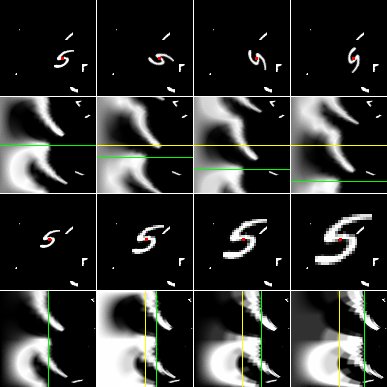
State-of-the-art deep learning systems often require large amounts of data and computation. For this reason, leveraging known or unknown structure of the data is paramount. Convolutional neural networks (CNNs) are successful examples of this principle, their defining characteristic being the shift-equivariance. By sliding a filter over the input, when the input shifts, the response shifts by the same amount, exploiting the structure of natural images where semantic content is independent of absolute pixel positions. This property is essential to the success of CNNs in audio, image and video recognition tasks. In this thesis, we extend equivariance to other kinds of transformations, such as rotation and scaling. We propose equivariant models for different transformations defined by groups of symmetries. The main contributions are (i) polar transformer networks, achieving equivariance to the group of similarities on the plane, (ii) equivariant multi-view networks, achieving equivariance to the group of symmetries of the icosahedron, (iii) spherical CNNs, achieving equivariance to the continuous 3D rotation group, (iv) cross-domain image embeddings, achieving equivariance to 3D rotations for 2D inputs, and (v) spin-weighted spherical CNNs, generalizing the spherical CNNs and achieving equivariance to 3D rotations for spherical vector fields. Applications include image classification, 3D shape classification and retrieval, panoramic image classification and segmentation, shape alignment and pose estimation. What these models have in common is that they leverage symmetries in the data to reduce sample and model complexity and improve generalization performance. The advantages are more significant on (but not limited to) challenging tasks where data is limited or input perturbations such as arbitrary rotations are present.
翻译:由于这个原因,利用已知或未知的数据结构是最重要的。 进化神经网络(CNNs)是这一原则的成功范例, 其定义特征是变换- 均匀。 当输入转换时, 通过在输入的过滤器上滑动一个过滤器, 反应会发生相同数量的变化, 利用自然图像的结构, 其中静态内容独立于绝对像素位置。 此属性对于CNN在音频、 图像和视频识别任务中的成功至关重要 。 在此理论中, 我们将变异性扩展至其他类型的变异, 如旋转和缩放。 我们提出由对调组定义的不同变异性变异性模型。 主要贡献是 (一) 极一般变异网络, 实现对平面相似组的变异性。 (二) 变异性多视图网络, 实现对等离异性、 变性变异性(三级分类) 的变异性变异性(三) 变异性网络的变异性变异性、变异性变异性变异性(三变异性调) 变变异性网络的变变异性变异性变异性、变变变变异(三变变变变变变变变异) 变的变变变变异性、变变变变的变的变变的变的变的变变变变变变异性、变的变的变变的变的变变变变变变变异性、变的变式、变式、变式、变式、变式、变式、变式、变式、变变异性、变式、变异性变式、变异性、变式、变异性、变式、变异性、变异性变异性、变异性的变式、变式、变式、变式、变式、变异性变式、变异性变式、变式、变式、变式、变式、变式、变式、变式、变式、变式、变式、变式、变式、变式、变变变式、变式、变式、变式、变式、变式、变式、变式、变式、变式、变式、变式、变式、变式、变式、变式、变式、