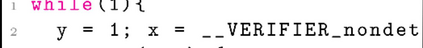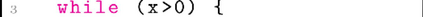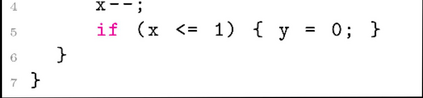Source-Level Bitwise Branching for Temporal Verification of Lifted Binaries

There is increasing interest in applying verification tools to programs that have bitvector operations (eg., binaries). SMT solvers, which serve as a foundation for these tools, have thus increased support for bitvector reasoning through bit-blasting and linear arithmetic approximations. In this paper we show that similar linear arithmetic approximation of bitvector operations can be done at the source level through transformations. Specifically, we introduce new paths that over-approximate bitvector operations with linear conditions/constraints, increasing branching but allowing us to better exploit the well-developed integer reasoning and interpolation of verification tools. We show that, for reachability of bitvector programs, increased branching incurs negligible overhead yet, when combined with integer interpolation optimizations, enables more programs to be verified. We further show this exploitation of integer interpolation in the common case also enables competitive termination verification of bitvector programs and leads to the first effective technique for LTL verification of bitvector programs. Finally, we provide an in-depth case study of decompiled ("lifted") binary programs, which emulate X86 execution through frequent use of bitvector operations. We present a new tool DarkSea, the first tool capable of verifying reachability, termination, and LTL of such lifted binaries.