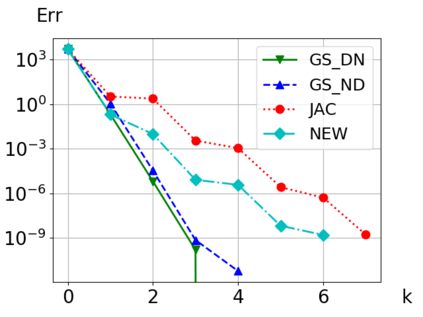
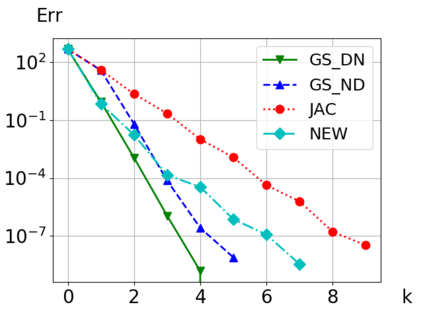
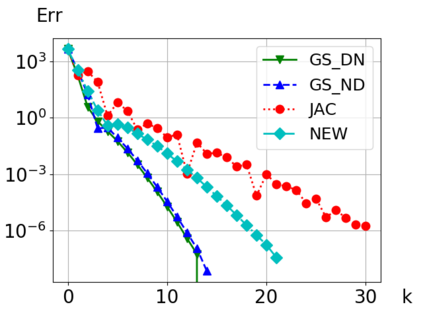
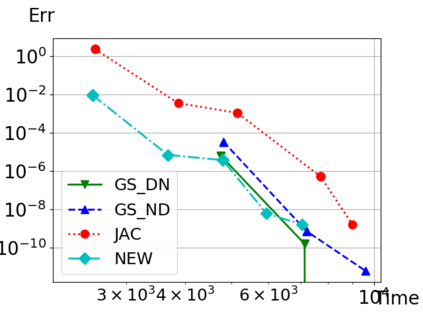
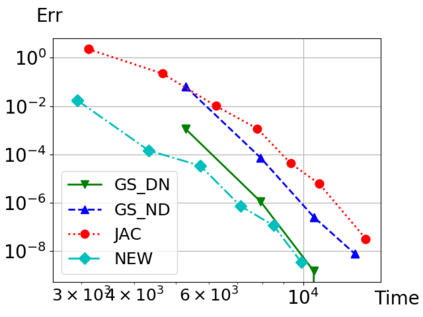
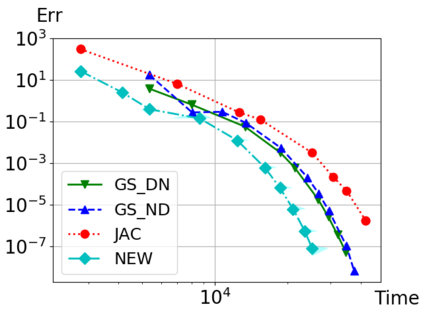
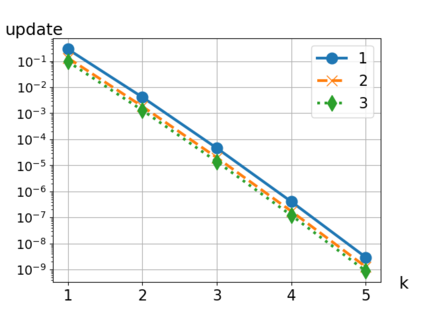
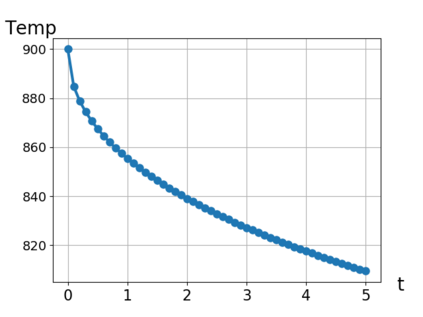
We consider Waveform Relaxation (WR) methods for partitioned time-integration of surface-coupled multiphysics problems. WR allows independent time-discretizations on independent and adaptive time-grids, while maintaining high time-integration orders. Classical WR methods such as Jacobi or Gauss-Seidel WR are typically either parallel or converge quickly. We present a novel parallel WR method utilizing asynchronous communication techniques to get both properties. Classical WR methods exchange discrete functions after time-integration of a subproblem. We instead asynchronously exchange time-point solutions during time-integration and directly incorporate all new information in the interpolants. We show both continuous and time-discrete convergence in a framework that generalizes existing linear WR convergence theory. An algorithm for choosing optimal relaxation in our new WR method is presented. Convergence is demonstrated in two conjugate heat transfer examples. Our new method shows an improved performance over classical WR methods. In one example we show a partitioned coupling of the compressible Euler equations with a nonlinear heat equation, with subproblems implemented using the open source libraries DUNE and FEniCS.
翻译:我们考虑的是波形放松(WW)方法,以分隔地表相混合的多物理学问题的时间整合。 WW允许独立和适应性时间网在独立和适应性时间网上独立的时间分解,同时保持高时间组合顺序。典型的典型的RW方法,如Jacobi或Gauss-Seidel WWW, 通常是平行的或快速的。我们提出了一个新的平行的WWS方法,利用无同步的通讯技术获得两种特性。经典的RW方法在子问题结合后交换离散功能。在时间组合期间,我们使用不同步的时间点交换时间点解决方案,直接将所有新信息纳入内极体。我们展示了连续和时间分解的RW趋同,在将现有的线性WS趋同理论普遍化的框架中,我们展示了选择我们新的RW方法的最佳放松的算法。在两个对调的热传输示例中展示了一致。我们的新方法显示古典的WRW方法的性能改进。在时间融合过程中,我们展示了对调的Eulnial-Flical等方程式进行分置的组合式组合式组合,同时使用非Eulnical-Els-e-eqlus 和已安装的开放的UN-e-Els-eqol-eqlent-eqluslveal-equal-eqpal-eqolpalpal-eqpal-eqal-eqal-lical-lical-dal-eqal-dalplical-lical-lical-lical-cal-lical-lical-lical-lical-lical-cal-lical-sal-sal-cal-cal-cal-cal-cal-cal-cal-cal-cal-cal-cal-calsal-sal-cal-cal-sal-sal-cal-e-e-e-e-e-e-e-e-e-e-e-e-e-e-e-e-e-e-e-e-e-e-e-eal-e-