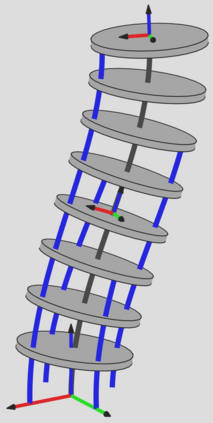
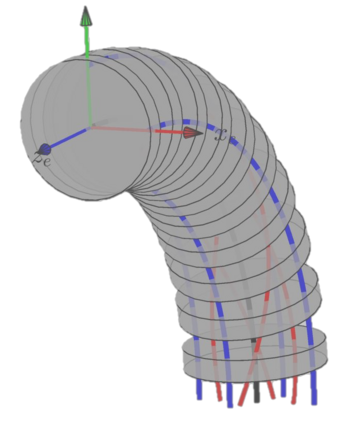
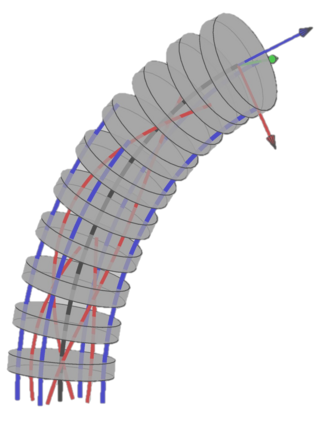
This paper considers a combination of actuation tendons and measurement strings to achieve accurate shape sensing and direct kinematics of continuum robots. Assuming general string routing, a methodical Lie group formulation for the shape sensing of these robots is presented. The shape kinematics is expressed using arc-length-dependent curvature distributions parameterized by modal functions, and the Magnus expansion for Lie group integration is used to express the shape as a product of exponentials. The tendon and string length kinematic constraints are solved for the modal coefficients and the configuration space and body Jacobian are derived. The noise amplification index for the shape reconstruction problem is defined and used for optimizing the string/tendon routing paths, and a planar simulation study shows the minimal number of strings/tendons needed for accurate shape reconstruction. A torsionally stiff continuum segment is used for experimental evaluation, demonstrating mean (maximal) end-effector absolute position error of less than 2% (5%) of total length. Finally, a simulation study of a torsionally compliant segment demonstrates the approach for general deflections and string routings. We believe that the methods of this paper can benefit the design process, sensing and control of continuum and soft robots.
翻译:本文考虑一系列活性图案和测量字符串的组合,以便实现连续机器人的精确形状感测和直接运动。 假设一般字符串路由, 将展示一个用于这些机器人形状感测的有条理的立体组配方。 形状动体学的表达方式是使用按模型函数设定的弧长依赖曲度分布参数表示, 而用于 Lie 组集的Magnus 扩展法用于表示形状, 表示成指数的产物。 圆形和弦线长度的运动力限制是针对模型系数和组合空间和体的。 形状重建问题的噪声振荡放大指数被确定并用于优化字符串/ tendon 路由路径, 以及一个平面模拟研究显示精确形状重建所需的最小数量的线状/ 线性分布。 实验性坚固的连续段用于表示形状, 显示总长度小于2%( 最大) 的断晶度绝对位置错误。 最后, 将产生组合空间和体体体空间和体体体体体组成。 的模拟研究将显示一般偏移偏移和连续线设计方法。