How Does the Task Landscape Affect MAML Performance?

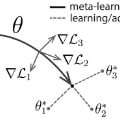
Model-Agnostic Meta-Learning (MAML) has become increasingly popular for training models that can quickly adapt to new tasks via one or few stochastic gradient descent steps. However, the MAML objective is significantly more difficult to optimize compared to standard Empirical Risk Minimization (ERM), and little is understood about how much MAML improves over ERM in terms of the fast adaptability of their solutions in various scenarios. We analytically address this issue in a linear regression setting consisting of a mixture of easy and hard tasks, where hardness is related to the condition number of the task's loss function. Specifically, we prove that in order for MAML to achieve substantial gain over ERM, (i) there must be some discrepancy in hardness among the tasks, and (ii) the optimal solutions of the hard tasks must be closely packed with the center far from the center of the easy tasks optimal solutions. We also give numerical and analytical results suggesting that these insights also apply to two-layer neural networks. Finally, we provide few-shot image classification experiments that support our insights for when MAML should be used and emphasize the importance of training MAML on hard tasks in practice.