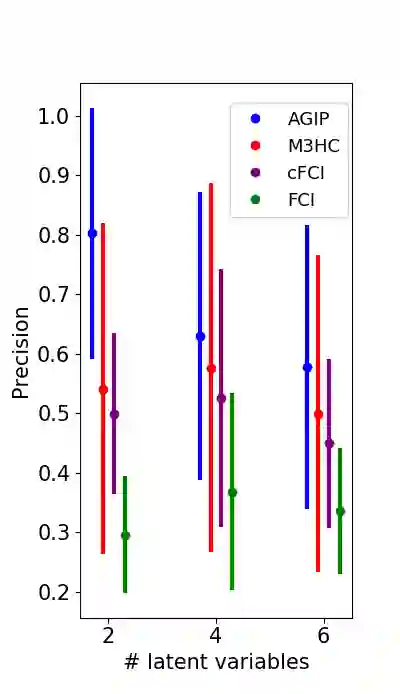
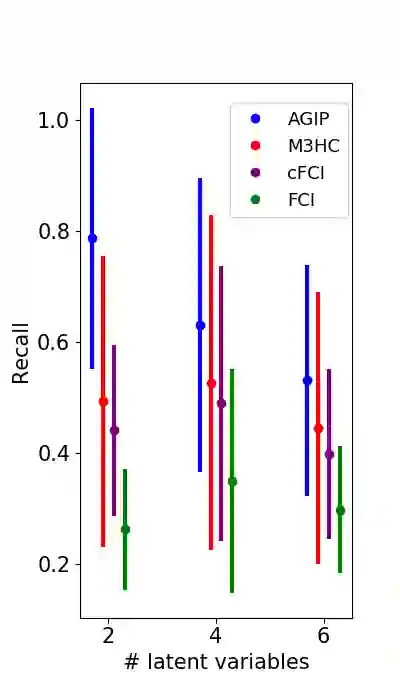
The problem of finding an ancestral acyclic directed mixed graph (ADMG) that represents the causal relationships between a set of variables is an important area of research on causal inference. Most existing score-based structure learning methods focus on learning directed acyclic graph (DAG) models without latent variables. A number of score-based methods have recently been proposed for the ADMG learning, yet they are heuristic in nature and do not guarantee an optimal solution. We propose a novel exact score-based method that solves an integer programming (IP) formulation and returns a score-maximizing ancestral ADMG for a set of continuous variables that follow a multivariate Gaussian distribution. We generalize the state-of-the-art IP model for DAG learning problems and derive new classes of valid inequalities to formulate an IP model for ADMG learning. Empirically, our model can be solved efficiently for medium-sized problems and achieves better accuracy than state-of-the-art score-based methods as well as benchmark constraint-based methods.
翻译:寻找祖传的环绕式定向混合图(ADMG)是一组变数之间的因果关系,这是对因果推断的一个重要研究领域。现有的基于分数的结构学习方法大多侧重于学习没有潜在变量的环绕式图(DAG)模型。最近为ADMG的学习提出了一些基于分数的方法,但这些方法在性质上是累赘的,不能保证最佳解决办法。我们提出了一种新的精确的基于分数的方法,解决了整数编程(IP)的配方,并返回了按多变量分布的一套连续变量的对等化祖传的ADMGMG。我们推广了DAG学习问题最先进的IP模型,并开发了有效的不平等新类别,为ADMG的学习设计了IP模型。我们的模式在中度问题上可以有效地解决,并且比基于分数的公式方法以及基于基准的制约方法更加精确。