Dissimilarity functions for rank-invariant hierarchical clustering of continuous variables

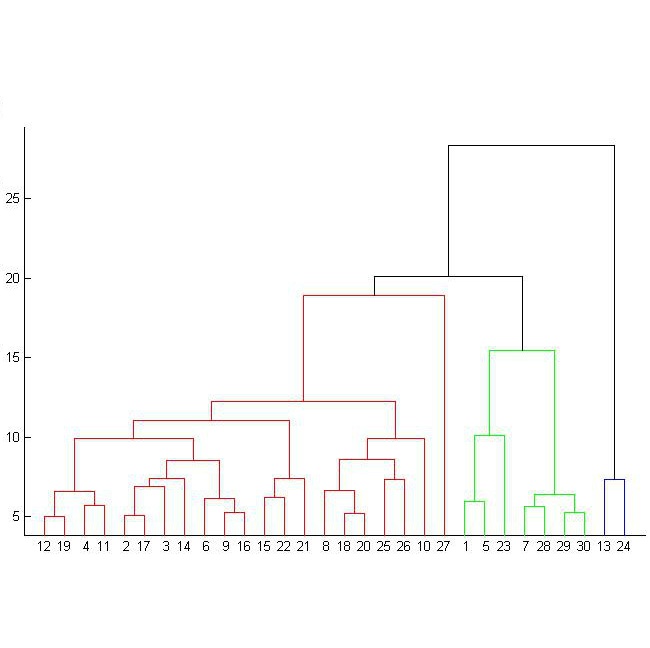
A theoretical framework is presented for a (copula-based) notion of dissimilarity between continuous random vectors and its main properties are studied. The proposed dissimilarity assigns the smallest value to a pair of random vectors that are comonotonic. Various properties of this dissimilarity are studied, with special attention to those that are prone to the hierarchical agglomerative methods, such as reducibility. Some insights are provided for the use of such a measure in clustering algorithms and a simulation study is presented. Real case studies illustrate the main features of the whole methodology.