Existence, uniqueness, and convergence rates for gradient flows in the training of artificial neural networks with ReLU activation

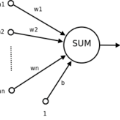
The training of artificial neural networks (ANNs) with rectified linear unit (ReLU) activation via gradient descent (GD) type optimization schemes is nowadays a common industrially relevant procedure. Till this day in the scientific literature there is in general no mathematical convergence analysis which explains the numerical success of GD type optimization schemes in the training of ANNs with ReLU activation. GD type optimization schemes can be regarded as temporal discretization methods for the gradient flow (GF) differential equations associated to the considered optimization problem and, in view of this, it seems to be a natural direction of research to first aim to develop a mathematical convergence theory for time-continuous GF differential equations and, thereafter, to aim to extend such a time-continuous convergence theory to implementable time-discrete GD type optimization methods. In this article we establish two basic results for GF differential equations in the training of fully-connected feedforward ANNs with one hidden layer and ReLU activation. In the first main result of this article we establish in the training of such ANNs under the assumption that the probability distribution of the input data of the considered supervised learning problem is absolutely continuous with a bounded density function that every GF differential equation admits for every initial value a solution which is also unique among a suitable class of solutions. In the second main result of this article we prove in the training of such ANNs under the assumption that the target function and the density function of the probability distribution of the input data are piecewise polynomial that every non-divergent GF trajectory converges with an appropriate rate of convergence to a critical point and that the risk of the non-divergent GF trajectory converges with rate 1 to the risk of the critical point.