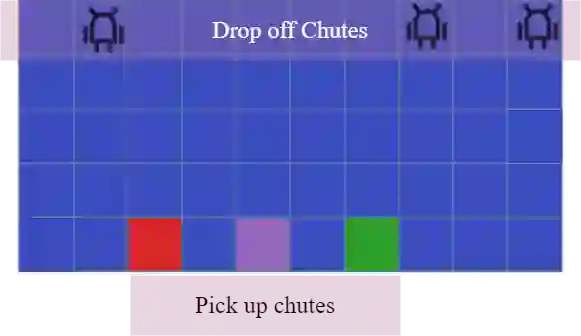
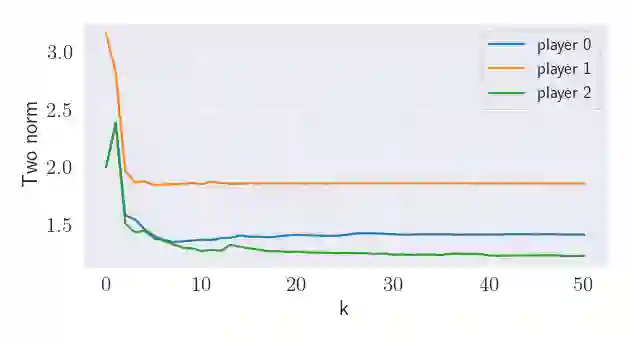
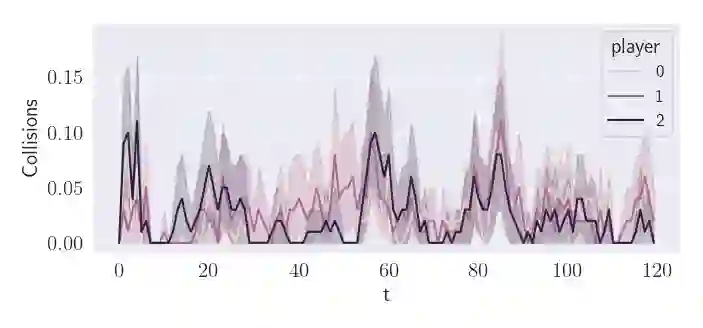
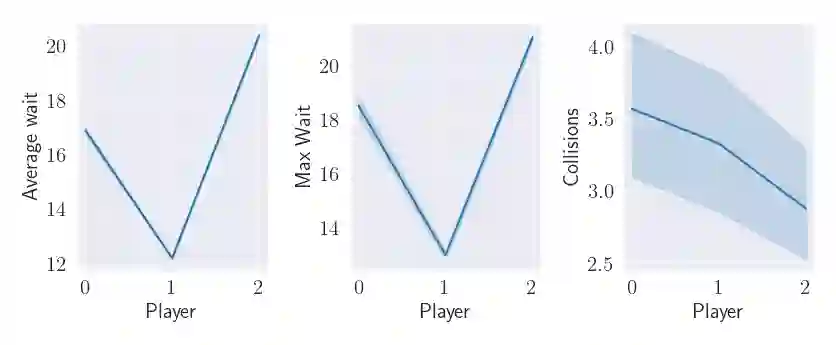
Inspired by the path coordination problem arising from robo-taxis, warehouse management, and mixed-vehicle routing problems, we model a group of heterogeneous players responding to stochastic demands as a congestion game under Markov decision process dynamics. Players share a common state-action space but have unique transition dynamics, and each player's unique cost is a {function} of the joint state-action probability distribution. For a class of player cost functions, we formulate the player-specific optimization problem, prove the equivalence between the Nash equilibrium and the solution of a potential minimization problem, and derive dynamic programming approaches to solve the Nash equilibrium. We apply this game to model multi-agent path coordination and introduce congestion-based cost functions that enable players to complete individual tasks while avoiding congestion with their opponents. Finally, we present a learning algorithm for finding the Nash equilibrium that has linear complexity in the number of players. We demonstrate our game model on a multi-robot warehouse \change{path coordination problem}, in which robots autonomously retrieve and deliver packages while avoiding congested paths.
翻译:受Robo-taxis、仓库管理和混合车辆路由问题引起的路径协调问题的影响,我们以马可夫决定程序动态下的阻塞游戏的形式,将一组对随机需求作出反应的不同角色模拟成一组。玩家共享一个共同的州-行动空间,但具有独特的过渡动态,每个玩家的独特成本是州-行动联合概率分布的{功能}。对于一组玩家成本功能,我们设计了播放器特有的优化问题,证明了纳什平衡与潜在最小化问题的解决方案之间的等同性,并提出了解决纳什平衡的动态编程方法。我们应用了这个游戏来模拟多剂路径协调,并引入了基于拥挤的成本功能,使玩家既能完成个人任务,同时又避免与对手的拥堵。最后,我们提出了一个学习算法,以找到在玩家数量上具有线性复杂性的纳什平衡。我们展示了多机器人仓库的游戏模型 。