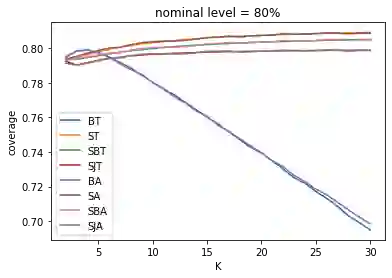
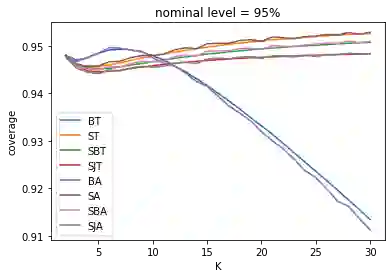
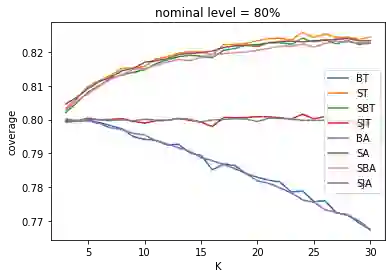
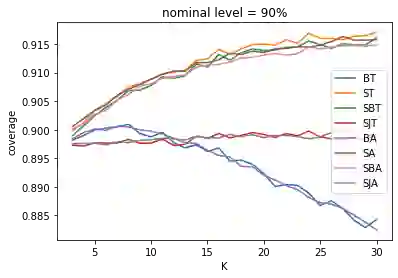
While batching methods have been widely used in simulation and statistics, it is open regarding their higher-order coverage behaviors and whether one variant is better than the others in this regard. We develop techniques to obtain higher-order coverage errors for batching methods by building Edgeworth-type expansions on $t$-statistics. The coefficients in these expansions are intricate analytically, but we provide algorithms to estimate the coefficients of the $n^{-1}$ error term via Monte Carlo simulation. We provide insights on the effect of the number of batches on the coverage error where we demonstrate generally non-monotonic relations. We also compare different batching methods both theoretically and numerically, and argue that none of the methods is uniformly better than the others in terms of coverage. However, when the number of batches is large, sectioned jackknife has the best coverage among all.
翻译:虽然在模拟和统计中广泛使用了批量方法,但对于其较高级的覆盖行为以及其中一种变量在这方面是否优于其他变量持开放态度。我们开发了方法,通过在美元统计学上建立 Edgeworth 型扩展来获取批量方法的较高级覆盖错误。这些扩展中的系数在分析上是复杂的,但我们提供了算法来估计通过蒙特卡洛模拟得出的$n ⁇ -1美元错误术语的系数。我们提供了对批量数对覆盖错误的影响的洞察力,我们展示了一般非单调关系。我们还从理论上和数字上比较了不同的批量方法,并争论说这些方法在覆盖方面没有一种统一优于其他方法。然而,当批量数量大时,分节型的千叶子的覆盖范围最大。