Fairer LP-based Online Allocation

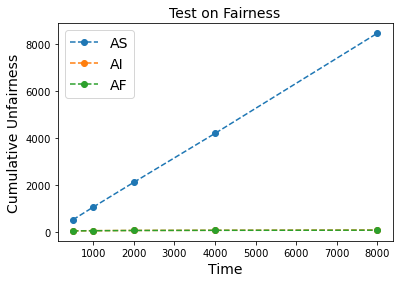
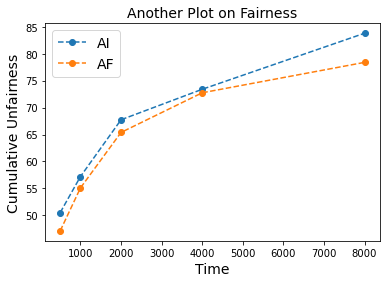
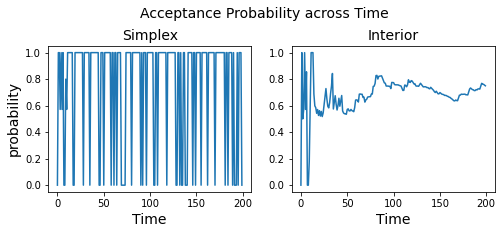
In this paper, we consider a Linear Program (LP)-based online resource allocation problem where a decision maker accepts or rejects incoming customer requests irrevocably in order to maximize expected revenue given limited resources. At each time, a new order/customer/bid is revealed with a request of some resource(s) and a reward. We consider a stochastic setting where all the orders are i.i.d. sampled from an unknown distribution. Such formulation contains many classic applications such as the canonical (quantity-based) network revenue management problem and the Adwords problem. Specifically, we study the objective of providing fairness guarantees while maintaining low regret. Our definition of fairness is that a fair online algorithm should treat similar agents/customers similarly and the decision made for similar individuals should be consistent over time. We define a fair offline solution as the analytic center of the offline optimal solution set, and propose a fair algorithm that uses an interior-point LP solver and dynamically detects unfair resource spending. Our algorithm can control cumulative unfairness (the cumulative deviation from the online solutions to the offline fair solution) on the scale of order $O(\log(T))$, while maintaining the regret to be bounded with dependency on $T$. Our approach do not formulate the fairness requirement as a constrain in the optimization instance, and instead we address the problem from the perspective of algorithm design. We get the desirable fairness guarantee without imposing any fairness constraint, and our regret result is strong for the reason that we evaluate the regret by comparing to the original objective value.