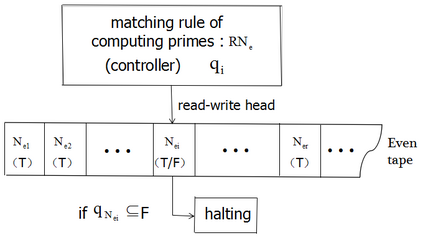
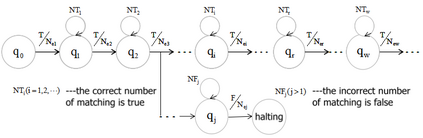
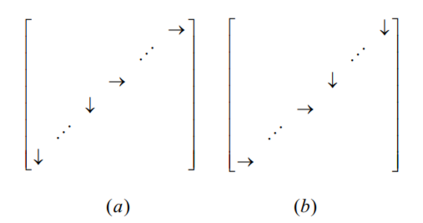
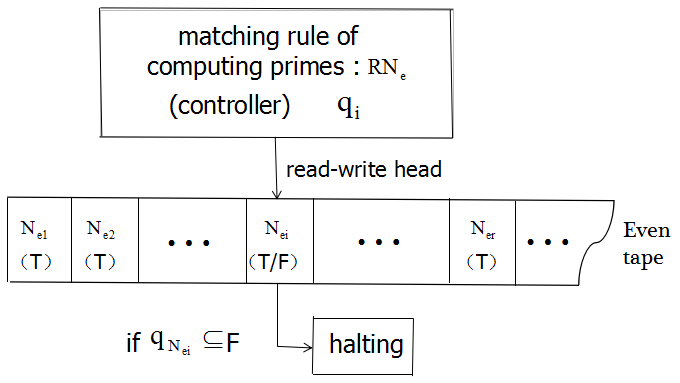
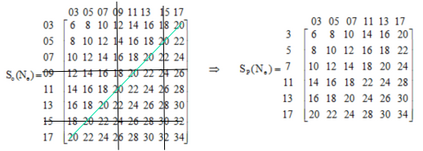Based on the propositional description of even Goldbach conjecture, in order to verify the truth of even Goldbach conjecture, we will deeply discuss this question and present a new computing model of $G{{N}_{e}}TM$ Turing Machine. This paper proves the infinite existence of even Goldbach's conjecture and obtains the following new results: 1. The criterion of general probability speculation of the existence judgment for even Goldbach conjecture is studied, and which at least have a formula satisfy the deduction result of matching requirements for even Goldbach conjecture in the model $\bmod \overset{\equiv }{\mathop{M}}\,({{N}_{e}})$. 2. In the controller of the $G{{N}_{e}}TM$ model, the algorithm problem of the prime matching rule is given, regardless of whether the computer can be recursively solved, the rule algorithm for designing prime numbers in controllers is computer recursively solvable. 3. The judgment problem that about even Goldbach conjecture whether infinite existence is studied. The new research result has shown that according to the constitution model of the full arranged matrix of given even number ${N}_{e}$, and if only given an even number ${N}_{e}$, it certainly exists the matrix model $Mod\overset{\equiv }{\mathop{X}}\,(p)$ and is proved to be equivalent. Therefore, it proves indirectly that the model $G{{N}_{e}}TM$ does not exist halting problem, and it also indicate that the even Goldbach conjecture is infinity existence.
翻译:基于甚至Goldbach预测的假设, 为了核实甚至Goldbach预测的真实性, 我们将深入讨论这个问题, 并提出一个新的计算模型$G ⁇ N ⁇ ⁇ e ⁇ TM$图灵机。 本文证明了即使Goldbach的推测也无穷无尽存在, 并取得了以下新结果 : 1. 研究关于甚至Goldbach预测存在判断的一般概率推测标准, 至少有一个公式满足了在模型中甚至Goldbach对甚至Goldbach预测的间接要求的扣减结果 $$\ bmod\ overset $yquev $unquiv $unmathop{M} (\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\