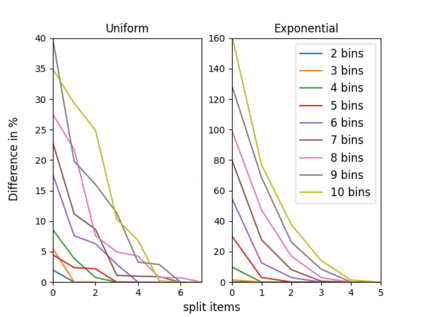
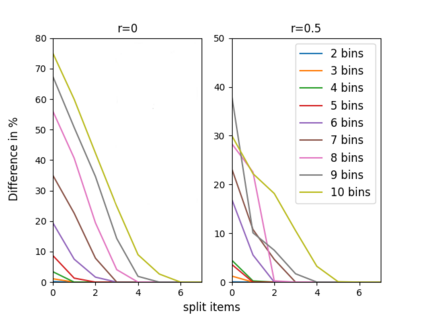
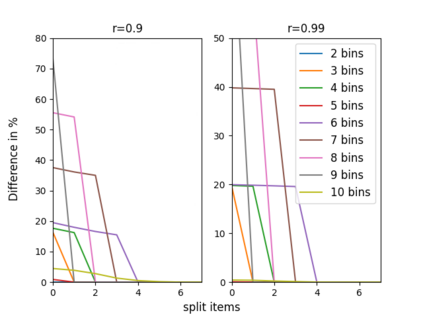
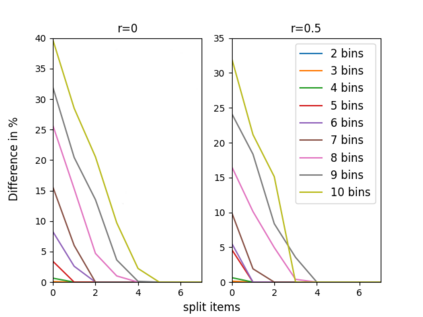
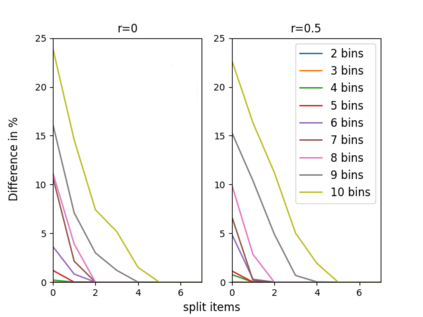
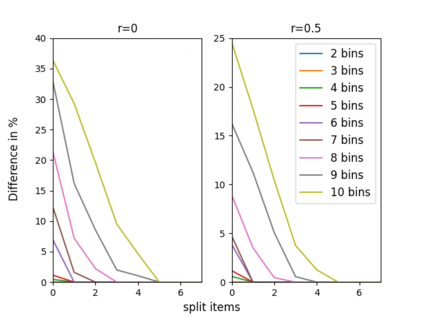
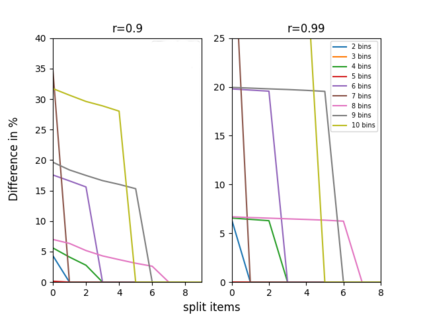
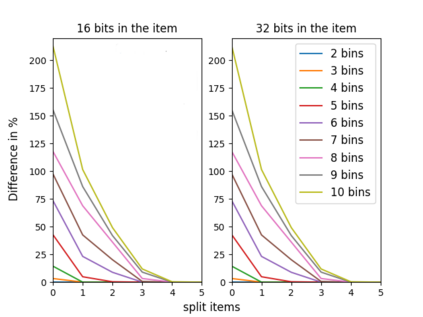
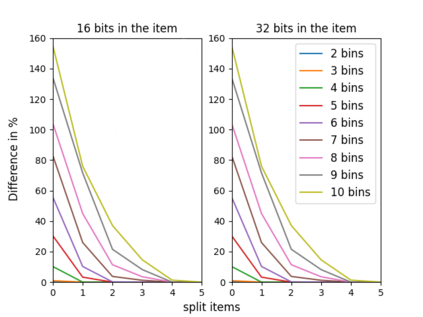
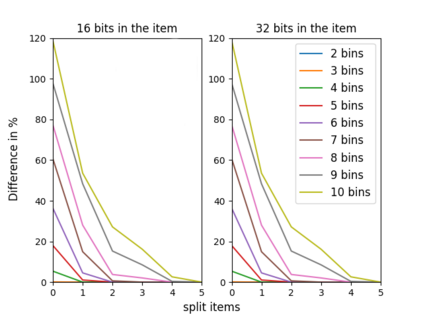
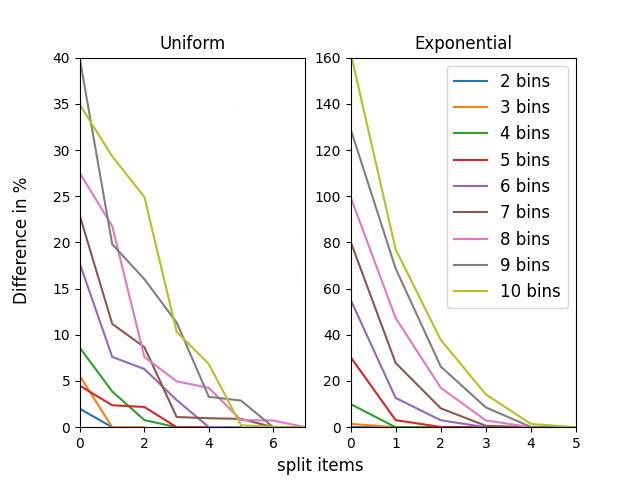
The n-way number partitioning problem, a fundamental challenge in combinatorial optimization, has significant implications for applications such as fair division and machine scheduling. Despite these problems being NP-hard, many approximation techniques exist. We consider three closely related kinds of approximations, and various objectives such as decision, min-max, max-min, and even a generalized objective, in which the bins are not considered identical anymore, but rather asymmetric (used to solve fair division to asymmetric agents or uniform machine scheduling problems). The first two variants optimize the partition such that: in the first variant some fixed number s of items can be split between two or more bins and in the second variant we allow at most a fixed number t of splittings. The third variant is a decision problem: the largest bin sum must be within a pre-specified interval, parameterized by a fixed rational number u times the largest item size. When the number of bins n is unbounded, we show that every variant is strongly NP-complete. When the number of bins n is fixed, the running time depends on the fixed parameters s,t,u. For each variant, we give a complete picture of its running time. For n=2, the running time is easy to identify. Our main results consider any fixed n>=3. Using a two-way polynomial-time reduction between the first and the third variant, we show that n-way number-partitioning with s split items can be solved in polynomial time if s>=n-2, and it is NP-complete otherwise. Also, n-way number-partitioning with t splittings can be solved in polynomial time if t>=n-1, and it is NP-complete otherwise. Finally, we show that the third variant can be solved in polynomial time if u>=(n-2)/n, and it is NP-complete otherwise. Our positive results for the optimization problems consider both asymmetric min-max and asymmetric max-min versions.
翻译:暂无翻译