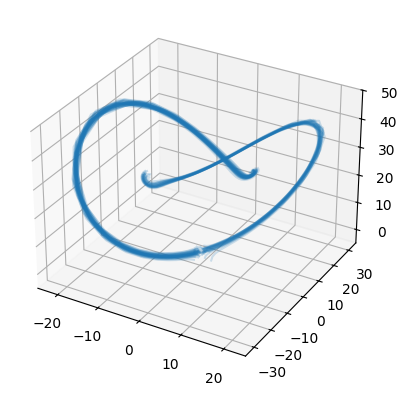
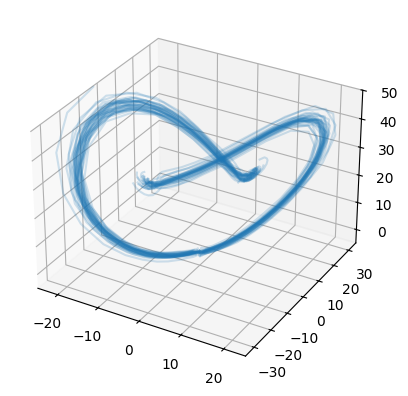
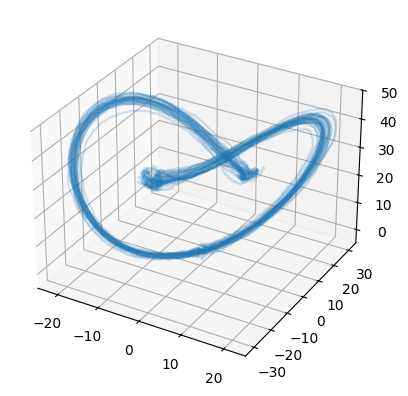
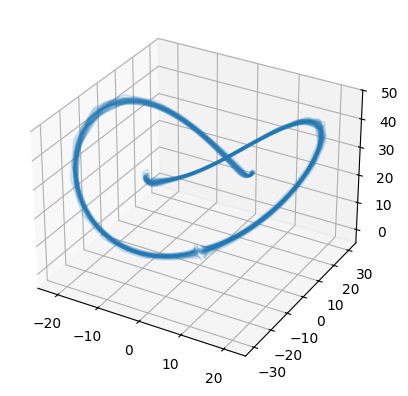
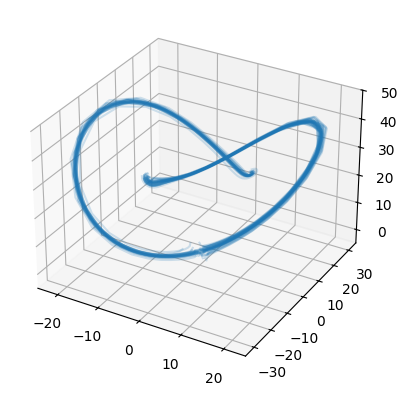
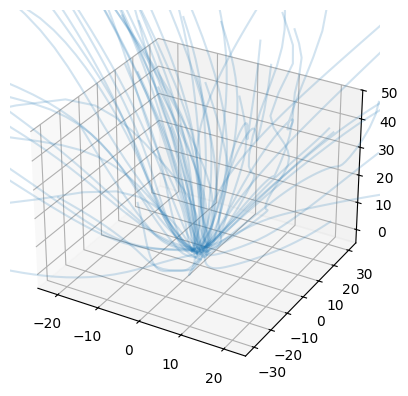
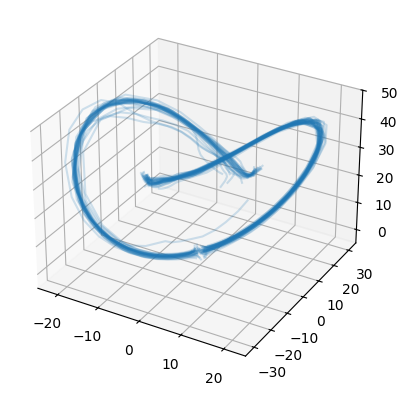
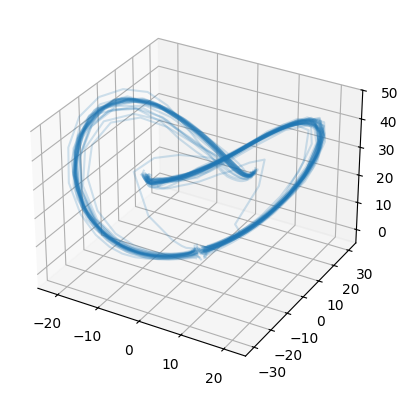
Stochastic differential equations (SDEs) are well suited to modelling noisy and irregularly sampled time series found in finance, physics, and machine learning. Traditional approaches require costly numerical solvers to sample between arbitrary time points. We introduce Neural Stochastic Flows (NSFs) and their latent variants, which directly learn (latent) SDE transition laws using conditional normalising flows with architectural constraints that preserve properties inherited from stochastic flows. This enables one-shot sampling between arbitrary states and yields up to two orders of magnitude speed-ups at large time gaps. Experiments on synthetic SDE simulations and on real-world tracking and video data show that NSFs maintain distributional accuracy comparable to numerical approaches while dramatically reducing computation for arbitrary time-point sampling.
翻译:暂无翻译