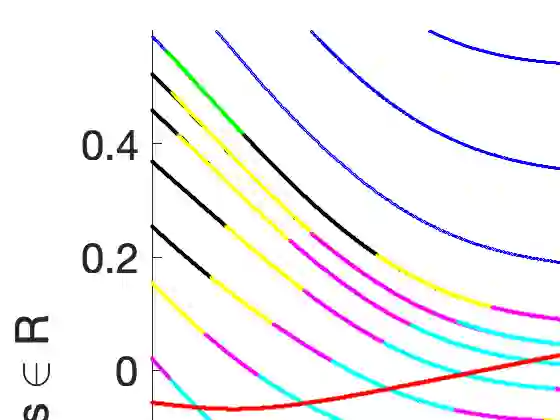
We present and implement an algorithm for computing the invariant circle and the corresponding stable manifolds for 2-dimensional maps. The algorithm is based on the parameterization method, and it is backed up by an a-posteriori theorem established in [YdlL21]. The algorithm works irrespective of whether the internal dynamics in the invariant circle is a rotation or it is phase-locked. The algorithm converges quadratically and the number of operations and memory requirements for each step of the iteration is linear with respect to the size of the discretization. We also report on the result of running the implementation in some standard models to uncover new phenomena. In particular, we explored a bundle merging scenario in which the invariant circle loses hyperbolicity because the angle between the stable directions and the tangent becomes zero even if the rates of contraction are separated. We also discuss and implement a generalization of the algorithm to 3 dimensions, and implement it on the 3-dimensional Fattened Arnold Family (3D-FAF) map with non-resonant eigenvalues and present numerical results.
翻译:我们为二维地图提出并实施一项计算变量圆和相应的稳定元数的算法。算法以参数化方法为基础,并辅之以在[YdlL21] 中建立的一个隐性定理。算法不管变异圆的内部动态是旋转的还是逐步封闭的,都起作用。算法将迭代的每个步骤的操作数量和内存要求相交,相对于离散的大小而言是线性的。我们还报告在某些标准模型中实施执行的结果,以发现新的现象。特别是,我们探索了一个捆绑式合并方案,使变异圆失去双向性,因为即使收缩速度分离,稳定方向和正切之间的角也变成零。我们还讨论并实施了3维的算法总化,并在3维的Fattened Arnold Form(3D-FAFAF)地图上执行,配有非共振的二元值和当前数字结果。