Tensor train completion: local recovery guarantees via Riemannian optimization

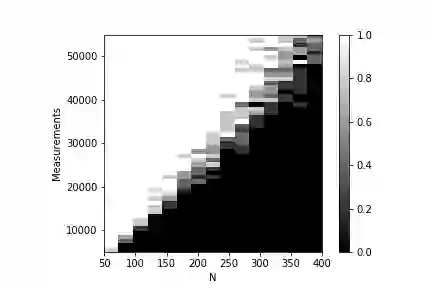
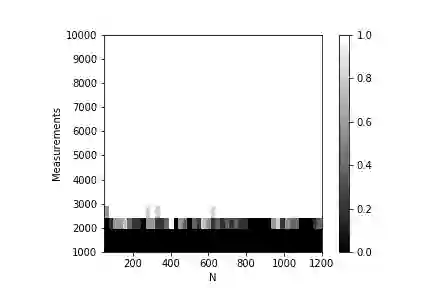
In this work we estimate the number of randomly selected elements of a tensor that with high probability guarantees local convergence of Riemannian gradient descent for tensor train completion. We derive a new bound for the orthogonal projections onto the tangent spaces based on the harmonic mean of the unfoldings' singular values and introduce a notion of core coherence for tensor trains. We also extend the results to tensor train completion with side information and obtain the corresponding local convergence guarantees.