An Information Bottleneck Problem with Rényi's Entropy

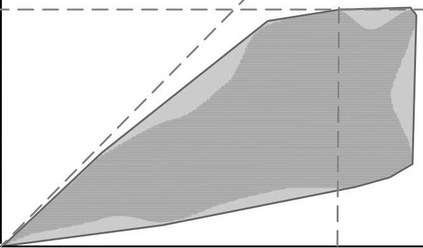
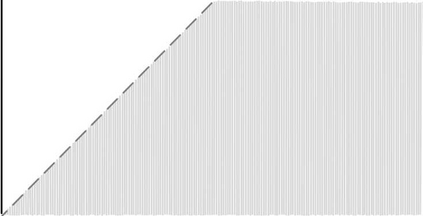
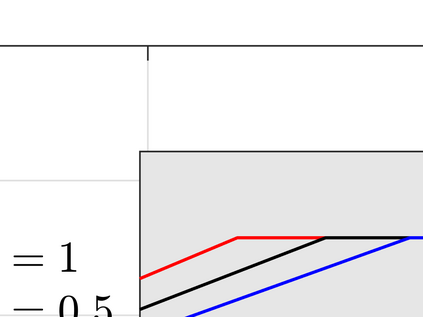
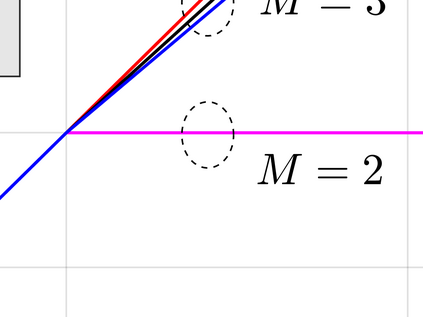
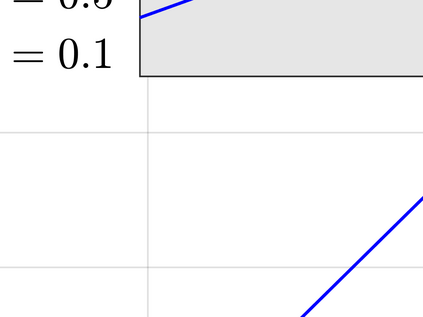
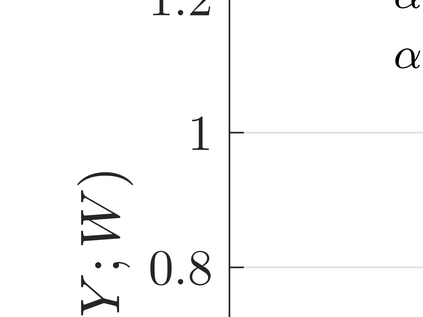
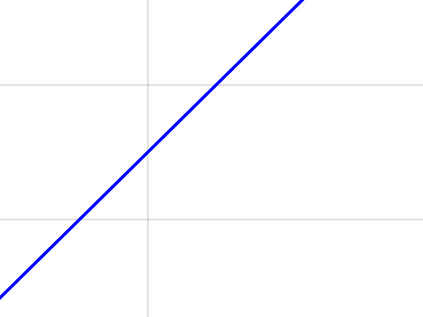
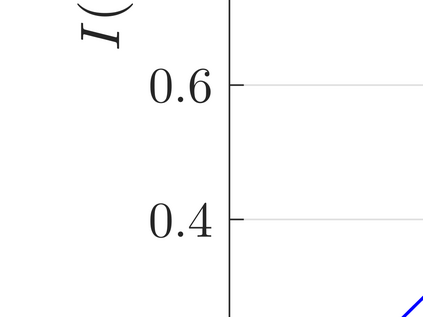
This paper considers an information bottleneck problem with the objective of obtaining a most informative representation of a hidden feature subject to a R\'enyi entropy complexity constraint. The optimal bottleneck trade-off between relevance (measured via Shannon's mutual information) and R\'enyi entropy cost is defined and an iterative algorithm for finding approximate solutions is provided. We also derive an operational characterization for the optimal trade-off by demonstrating that the optimal R\'enyi entropy-relevance trade-off is achievable by a simple time-sharing scalar coding scheme and that no coding scheme can provide better performance. Two examples where the optimal Shannon entropy-relevance trade-off can be exactly determined are further given.