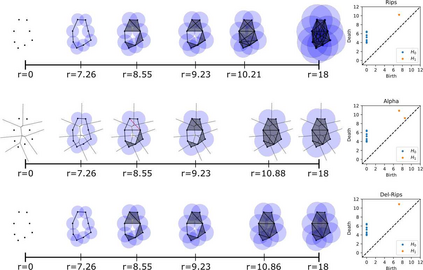
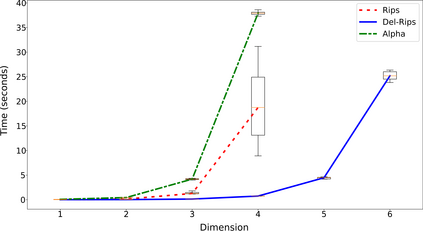
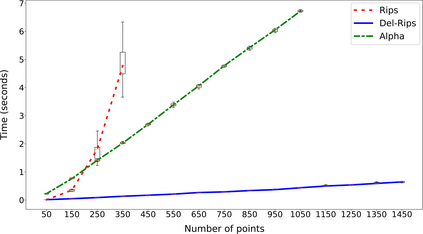
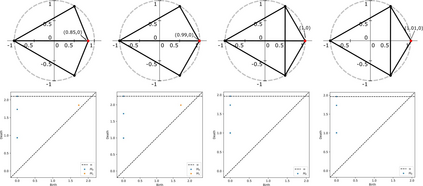
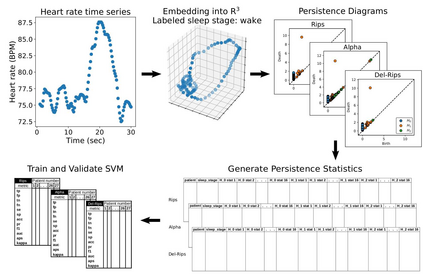
In this paper we define, implement, and investigate a simplicial complex construction for computing persistent homology of Euclidean point cloud data, which we call the Delaunay-Rips complex (DR). Assigning the Vietoris-Rips weights to simplices, DR experiences speed-up in the persistence calculations by only considering simplices that appear in the Delaunay triangulation of the point cloud. We document and compare a Python implementation of DR with other simplicial complex constructions for generating persistence diagrams. By imposing sufficient conditions on point cloud data, we are able to theoretically justify the stability of the persistence diagrams produced using DR. When the Delaunay triangulation of the point cloud changes under perturbations of the points, we prove that DR-produced persistence diagrams exhibit instability. Since we cannot guarantee that real-world data will satisfy our stability conditions, we demonstrate the practical robustness of DR for persistent homology in comparison with other simplicial complexes in machine learning applications. We find in our experiments that using DR for an ML-TDA pipeline performs comparatively well as using other simplicial complex constructions.
翻译:在本文中,我们定义、实施和调查了用于计算欧洲极点云数据持久性同质的简单复杂结构,我们称之为德劳奈-里普斯综合体。将越苏里-里普斯重量指定为不齐,DR经历在持久性计算中加速,仅考虑在德劳纳云三角中出现的不齐点。我们记录并比较了DR的Python实施过程与其他生成持久性图表的简单复杂结构的Python 实施过程。通过对点云数据施加足够的条件,我们可以理论上证明使用DR产生的持久性图的稳定性。当Delaunay对点云值的三角测量在点的扰动下显示点云值变化时,我们证明DR制作的持久性图表现出不稳定性。由于我们不能保证真实世界数据将满足我们的稳定条件,因此我们证明DR与其他机器学习复杂的系统相比,它具有实际的活力。我们在实验中发现,使用比较的ML-L-DR作为建设的复杂管道,我们用比较的ML-DR进行其他的建筑。</s>