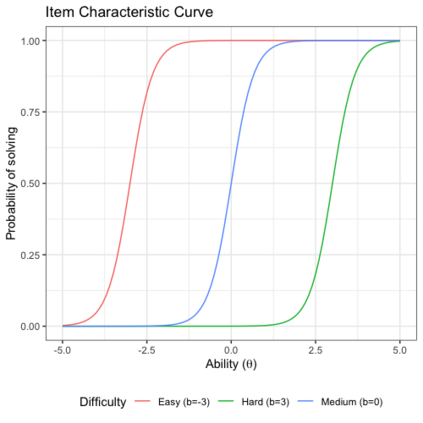
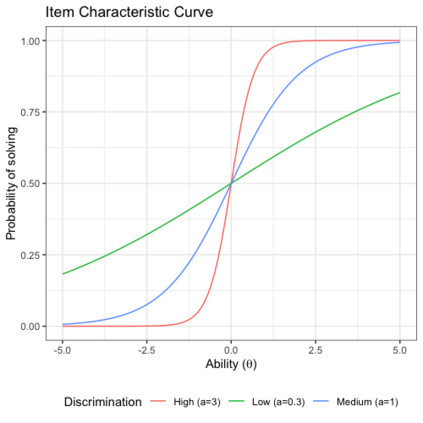
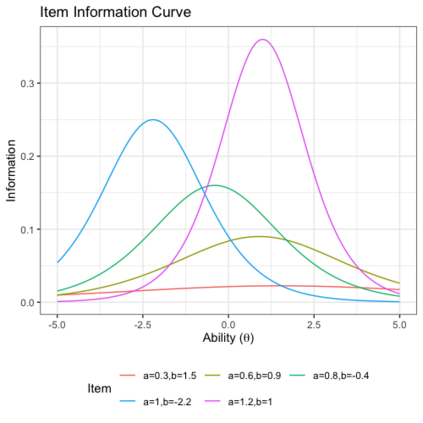
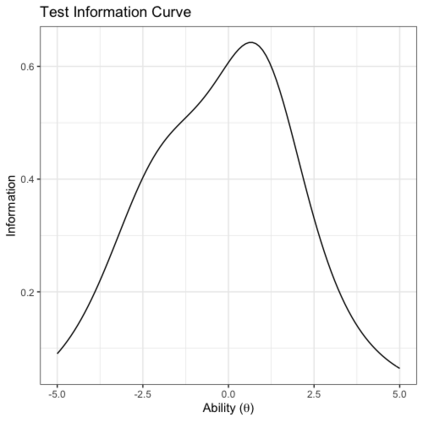
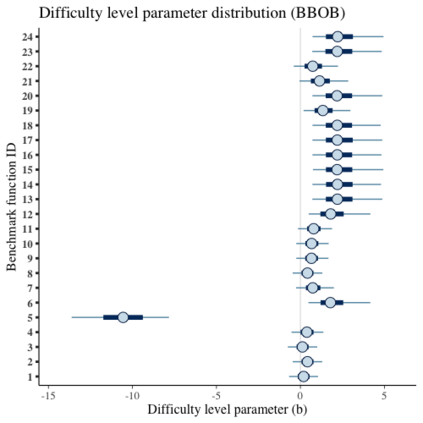
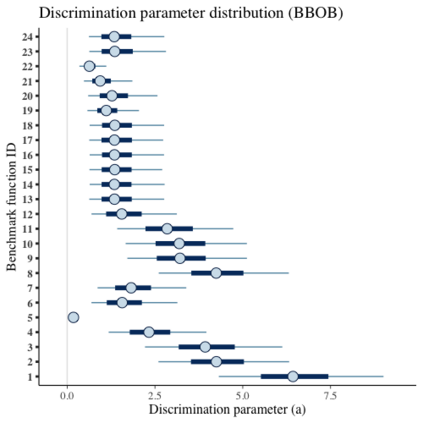
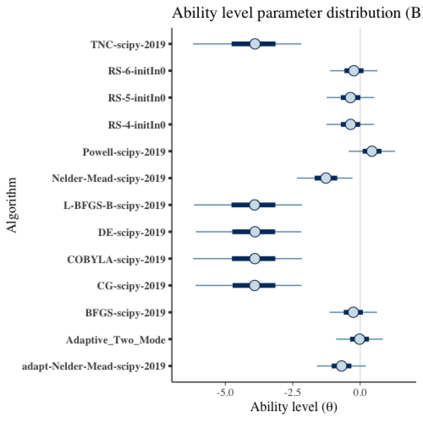
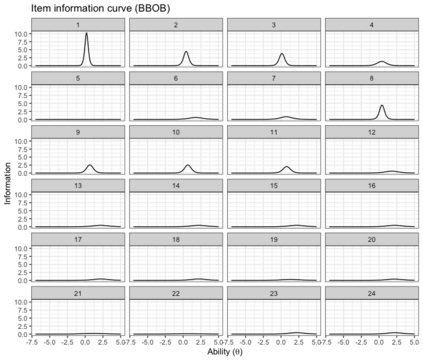
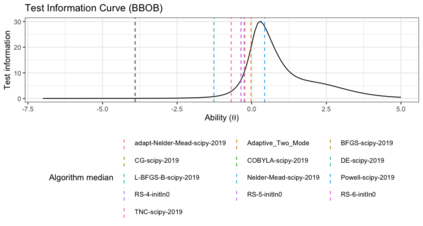
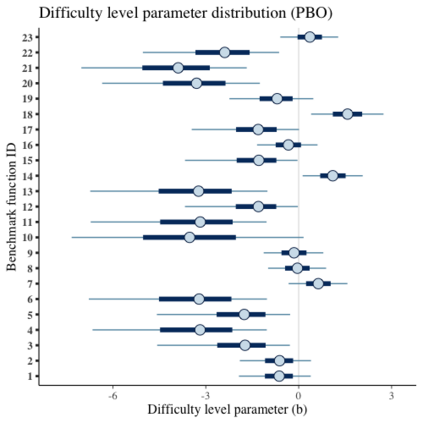
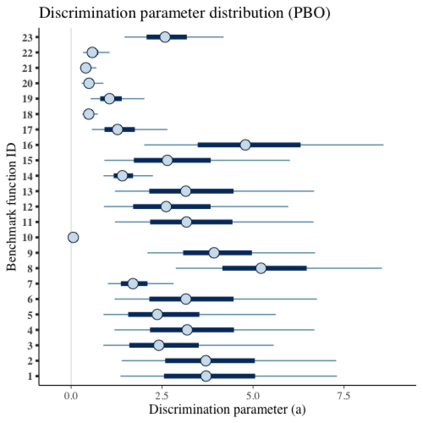
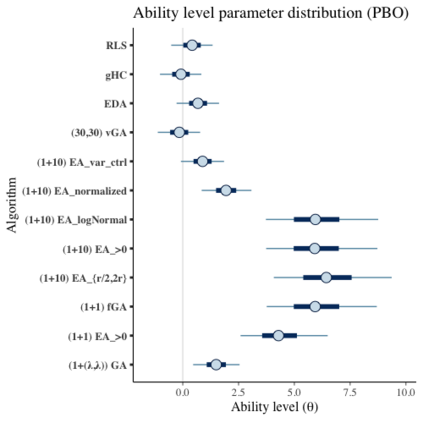
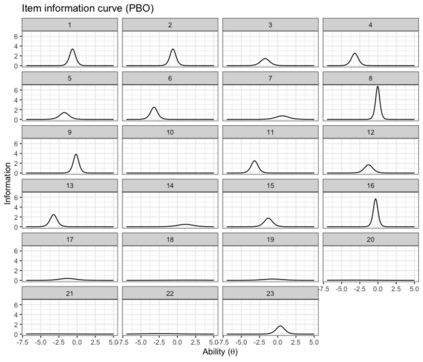
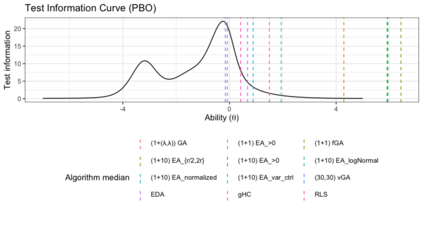
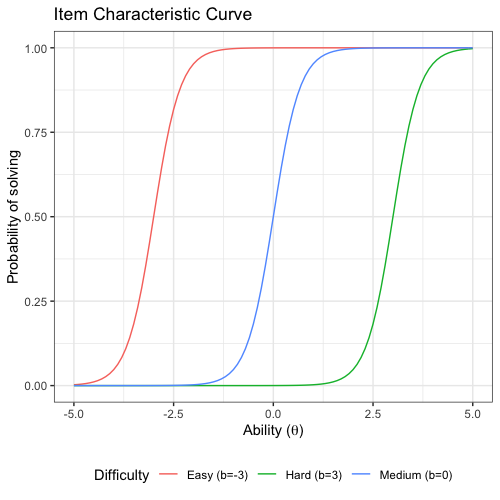
Benchmark suites, i.e. a collection of benchmark functions, are widely used in the comparison of black-box optimization algorithms. Over the years, research has identified many desired qualities for benchmark suites, such as diverse topology, different difficulties, scalability, representativeness of real-world problems among others. However, while the topology characteristics have been subjected to previous studies, there is no study that has statistically evaluated the difficulty level of benchmark functions, how well they discriminate optimization algorithms and how suitable is a benchmark suite for algorithm comparison. In this paper, we propose the use of an item response theory (IRT) model, the Bayesian two-parameter logistic model for multiple attempts, to statistically evaluate these aspects with respect to the empirical success rate of algorithms. With this model, we can assess the difficulty level of each benchmark, how well they discriminate different algorithms, the ability score of an algorithm, and how much information the benchmark suite adds in the estimation of the ability scores. We demonstrate the use of this model in two well-known benchmark suites, the Black-Box Optimization Benchmark (BBOB) for continuous optimization and the Pseudo Boolean Optimization (PBO) for discrete optimization. We found that most benchmark functions of BBOB suite have high difficulty levels (compared to the optimization algorithms) and low discrimination. For the PBO, most functions have good discrimination parameters but are often considered too easy. We discuss potential uses of IRT in benchmarking, including its use to improve the design of benchmark suites, to measure multiple aspects of the algorithms, and to design adaptive suites.
翻译:在比较黑箱优化算法时,广泛使用基准套件,即一套基准功能的集合。多年来,研究已经为基准套件确定了许多理想的品质,例如不同的地形学、不同的困难、可缩放性、真实世界问题的代表性等等。然而,虽然地形特征受以往研究的制约,但没有一项研究在统计上评估基准功能的困难程度、它们如何区别优化算法以及算法比较基准套件的适宜性。在本文中,我们提议使用一个项目响应理论(IRT)模型,即巴伊西亚两参数的逻辑逻辑模型,用于多次尝试,以便从统计角度评估这些方面的基准,与算法的经验成功率有关。但是,我们可以评估每个基准的难度,如何区别不同的算法,算法的能力分,以及基准套件在估算能力分数中增加了多少信息。我们用这个模型在两个广为人知的基准套件中,Bayesia-Box 基准(BBBOOO) 最易优化和BOBBA 最难度标准(BO Booim 最难程度) 和BO BO 最难的升级标准。我们用了BOBOBBA 最难度标准 最难的高级标准。我们找到BOBOBBBBBBBBBBBB 最难的高级标准 最难的高级标准的高级标准级标准级标准值。