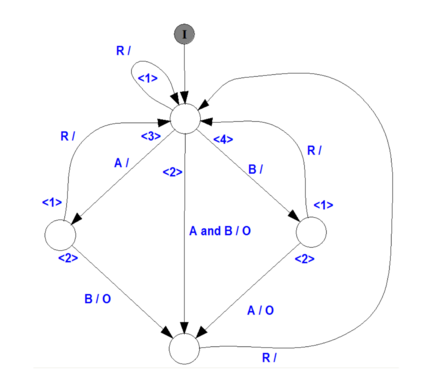
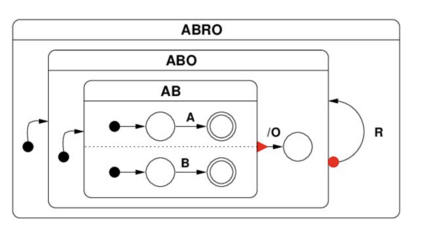
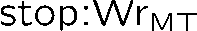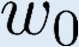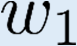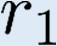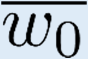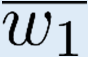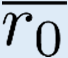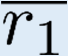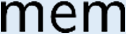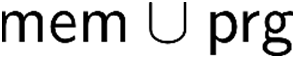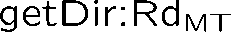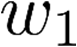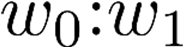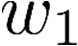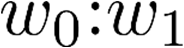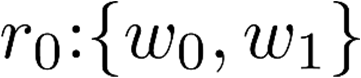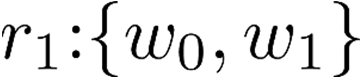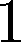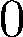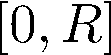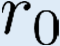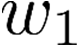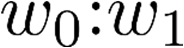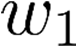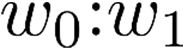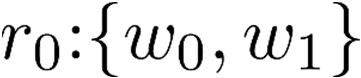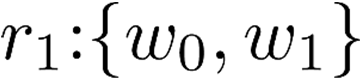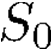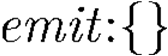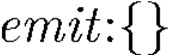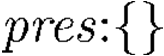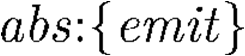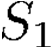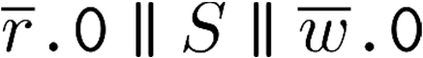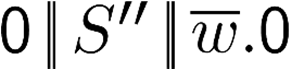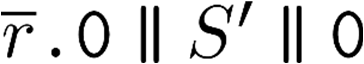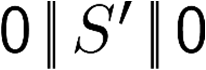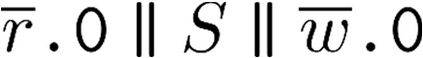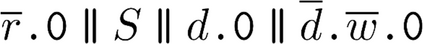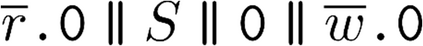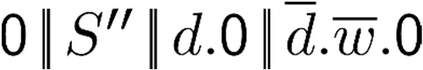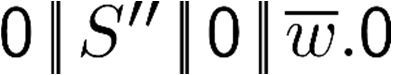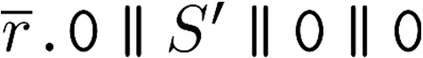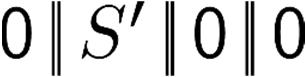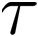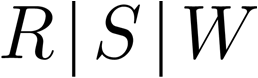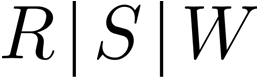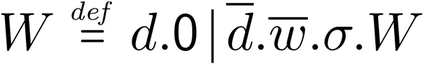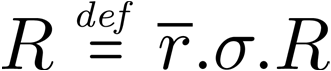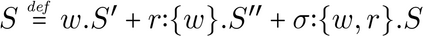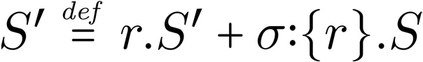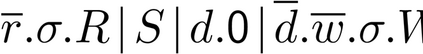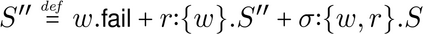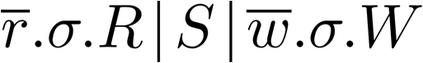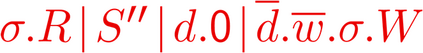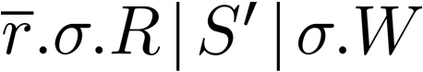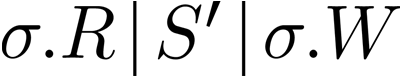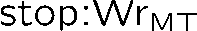Building on the standard theory of process algebra with priorities, we identify a new scheduling mechanism, called "constructive reduction" which is designed to capture the essence of synchronous programming. The distinctive property of this evaluation strategy is to achieve determinacy-by-construction for multi-cast concurrent communication with shared memory. In the technical setting of CCS extended by clocks and priorities, we prove for a large class of "coherent" processes a confluence property for constructive reductions. We show that under some restrictions, called "pivotability", coherence is preserved by the operators of prefix, summation, parallel composition, restriction and hiding. Since this permits memory and sharing, we are able to cover a strictly larger class of processes compared to those in Milner's classical confluence theory for CCS without priorities.
翻译:暂无翻译