Hamiltonian Cycle Problem is in P

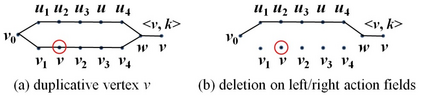
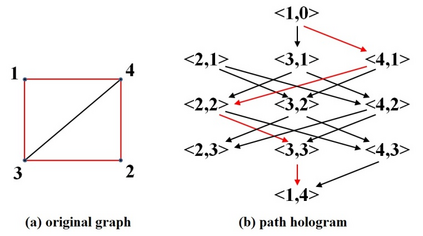
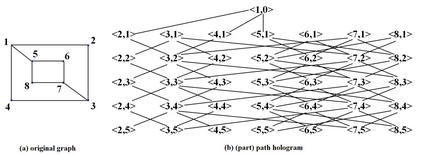
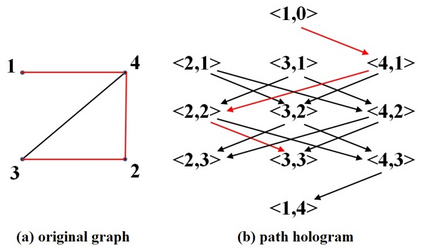
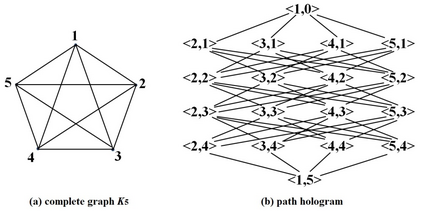
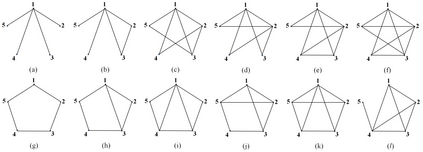
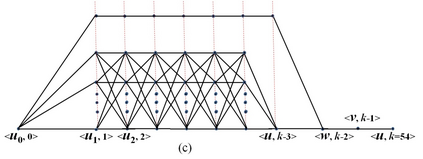
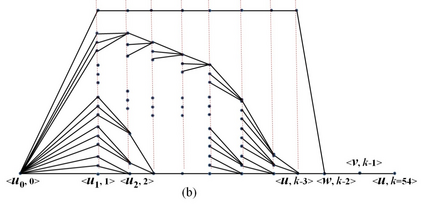
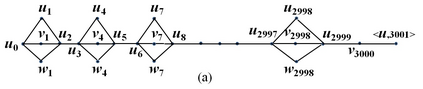
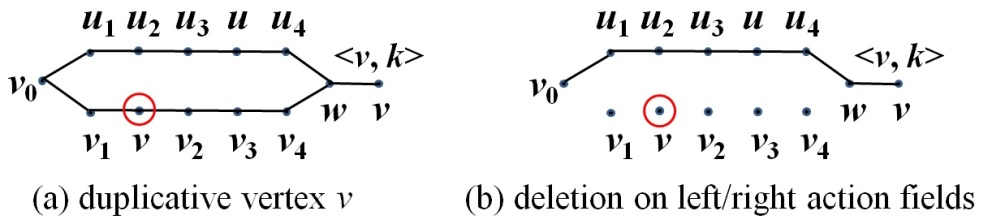
In this paper we present the first deterministic polynomial time algorithm for determining the existence of a Hamiltonian cycle and finding a Hamiltonian cycle in general graphs. Our algorithm can also resolve the Hamiltonian path problem in the traceable graphs. The space complexity of our algorithm is O(n^4). The time complexity are theoretically O(n^5*d^2) on average and O(n^6*d^2) in the worst case respectively, where d is the maximum degree of vertex. With parallel computing, the space complexity can be improved to O(n^3) and the time complexity to O(n^3*d^2) on average and O(n^4*d^2) in the worst case. We construct the corresponding path hologram transformed from the original graph and compute the path set, which is a collection of segment sets consisting of all the vertices located on the same segment layer among all the longest basic paths, of every vertex with dynamic programming. The path hologram is a multi-segment graph with the vertex <u, k> where u is a vertex and k is the segment layer of u in the path hologram. To ensure each path stored in the path set is legal and each segment set of the path set contains only valid vertices, the key strategy of our method is the "consecutive" deleting-replenishing operations recursively on the left/right action field of a vertex, respectively. The greatest contribution of our method is the path set in which all the legal paths can be stored in O(n^2) space for a complete graph of order n. In fact, our algorithm can be directly applied to the original graph. Besides, our algorithm can deal with the finite general graphs including undirected, directed, and mixed. As a result, the well-known problem HCP in NPC can be now resolved practically in deterministic polynomial time for general graphs in the worst case.