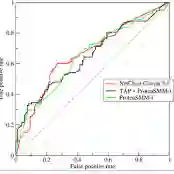
In this paper, we study multi-block min-max bilevel optimization problems, where the upper level is non-convex strongly-concave minimax objective and the lower level is a strongly convex objective, and there are multiple blocks of dual variables and lower level problems. Due to the intertwined multi-block min-max bilevel structure, the computational cost at each iteration could be prohibitively high, especially with a large number of blocks. To tackle this challenge, we present a single-loop randomized stochastic algorithm, which requires updates for only a constant number of blocks at each iteration. Under some mild assumptions on the problem, we establish its sample complexity of $O(1/\epsilon^4)$ for finding an $\epsilon$-stationary point. This matches the optimal complexity for solving stochastic nonconvex optimization under a general unbiased stochastic oracle model. Moreover, we provide two applications of the proposed method in multi-task deep AUC (area under ROC curve) maximization and multi-task deep partial AUC maximization. Experimental results validate our theory and demonstrate the effectiveness of our method on problems with hundreds of tasks.
翻译:在本文中,我们研究多区块最小和双层优化问题,即上层是非混凝土强凝固小型最大目标,下层是一个强烈的混凝土目标,并且存在多个两层变量和低层问题。由于多区块最小和双层结构相互交织,每次迭代的计算成本可能高得令人望而却步,特别是许多块。为了应对这一挑战,我们提出了一个单环随机随机随机随机蒸汽算法,该算法要求每个迭代只更新固定数块。在对问题的一些轻度假设下,我们确定其样本复杂性为O(1/\epsilon4)美元,用于寻找一个$\epslon$-固定点。这与在一般的不偏倚透视或触角模型下解决随机不相容非对称优化的最佳复杂程度相匹配。此外,我们提供了两种在多层深层ACUC(ROC曲线下的区域)中拟议方法的应用,即最大化和多层部分部分AUC最大化。我们数百项实验结果的理论验证和数百项任务存在问题。