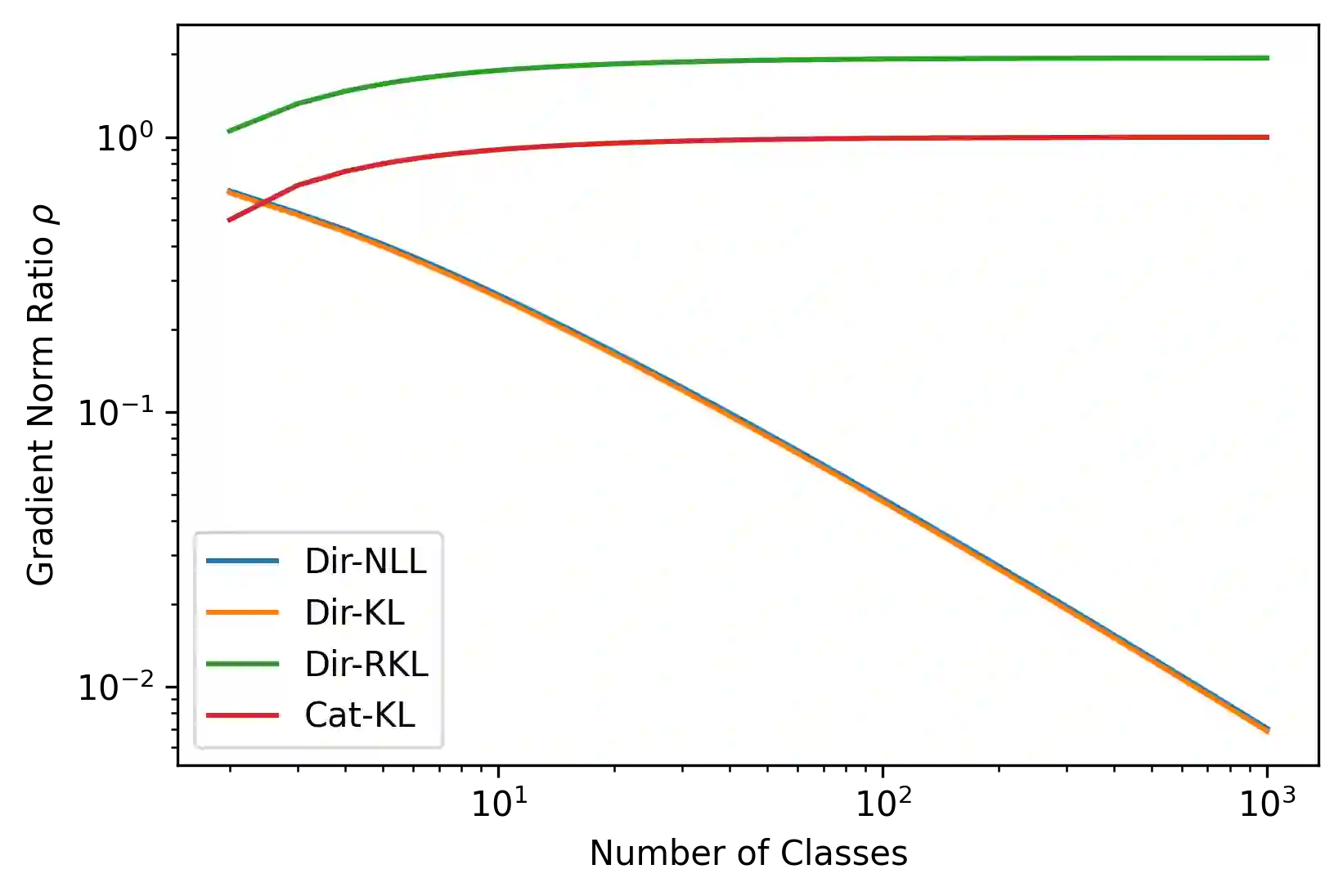
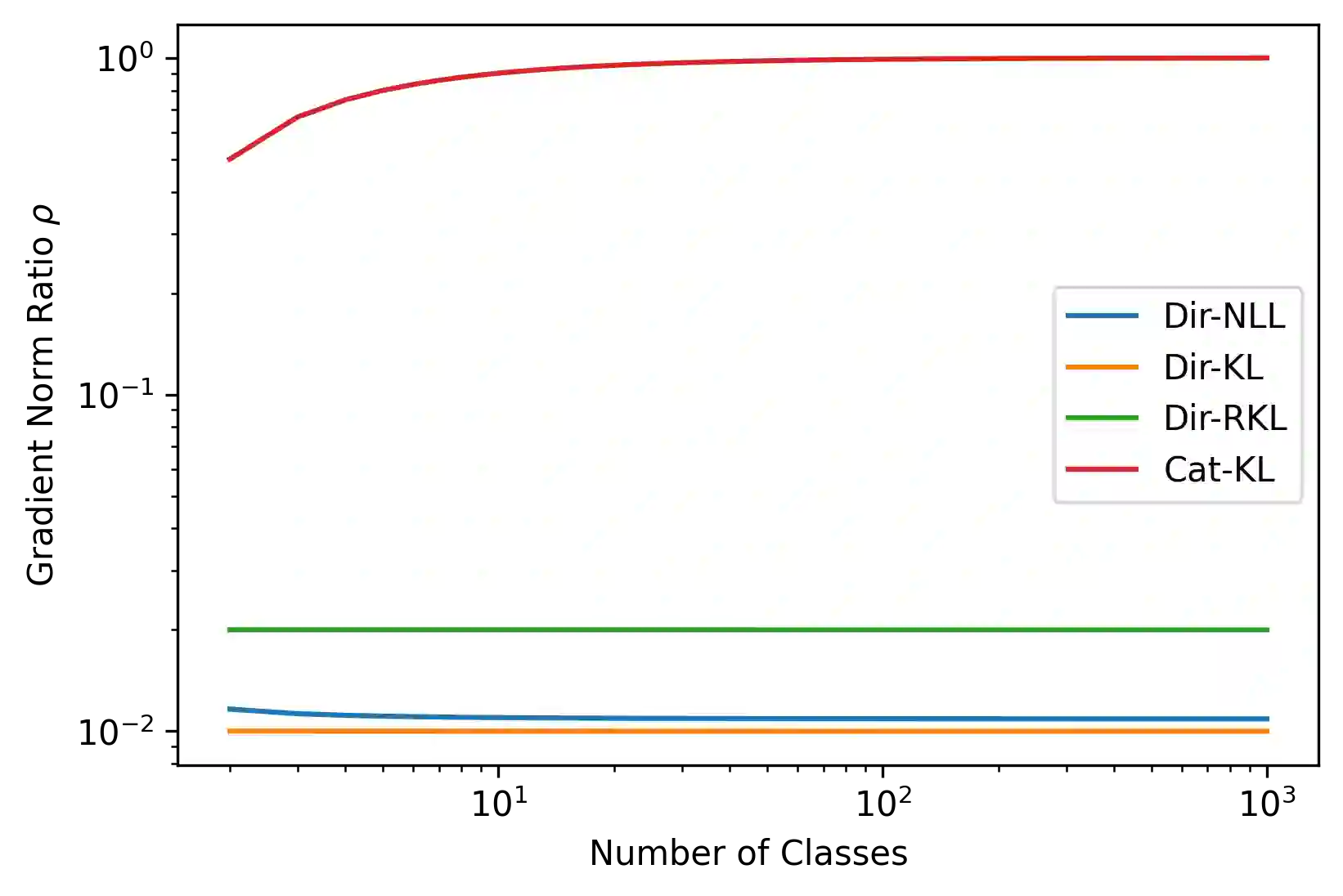
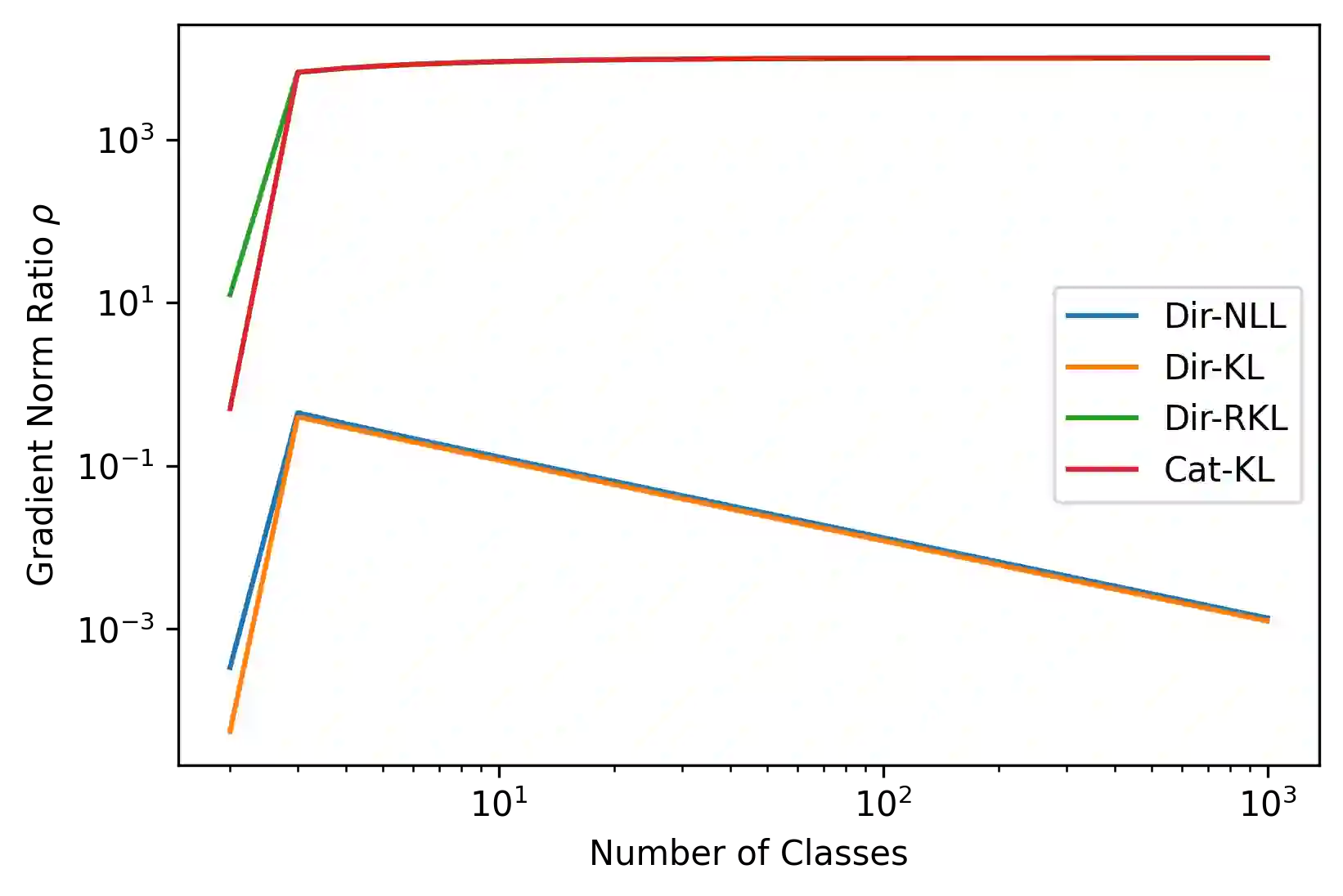
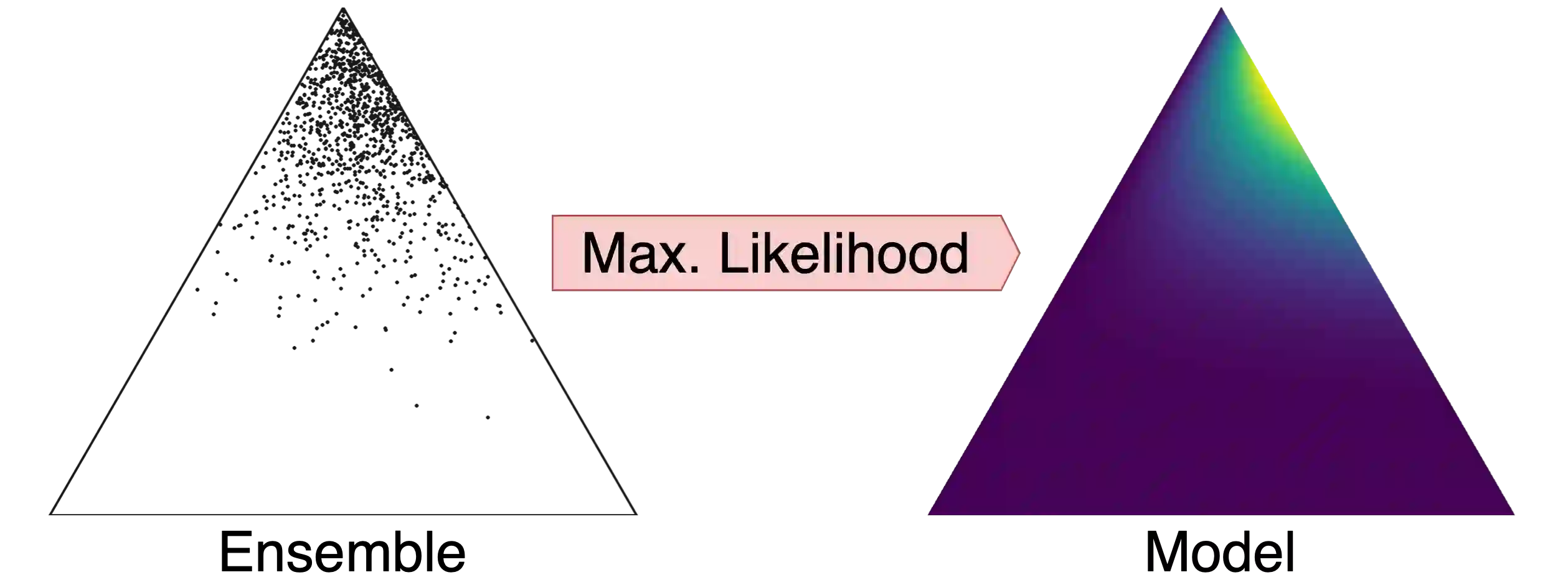
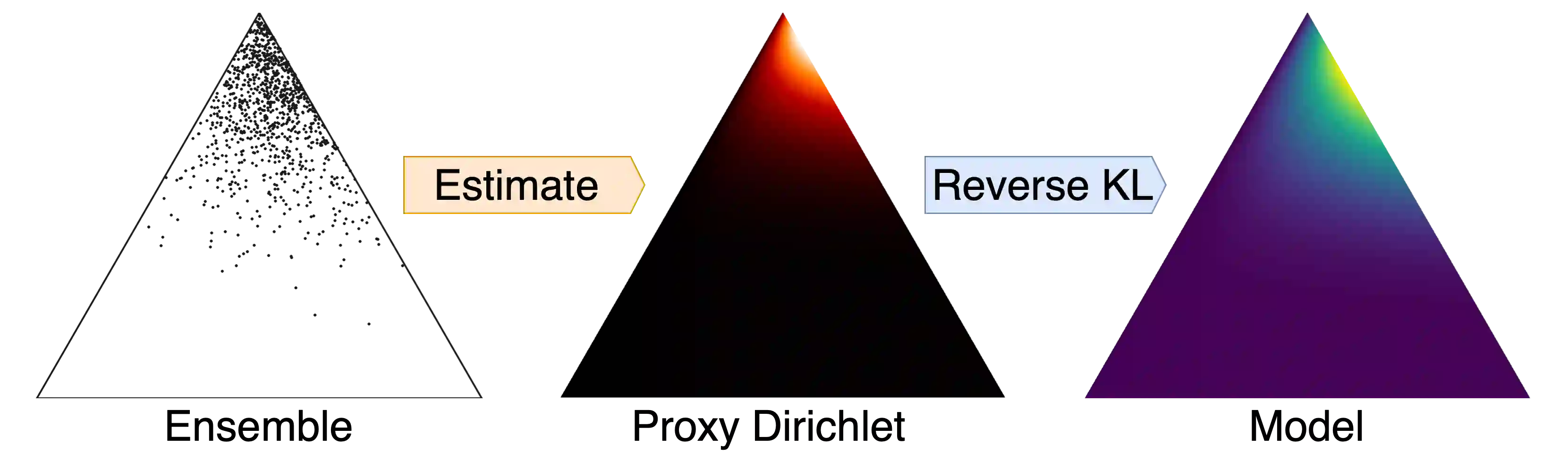
Ensembles of machine learning models yield improved system performance as well as robust and interpretable uncertainty estimates; however, their inference costs may often be prohibitively high. \emph{Ensemble Distribution Distillation} is an approach that allows a single model to efficiently capture both the predictive performance and uncertainty estimates of an ensemble. For classification, this is achieved by training a Dirichlet distribution over the ensemble members' output distributions via the maximum likelihood criterion. Although theoretically principled, this criterion exhibits poor convergence when applied to large-scale tasks where the number of classes is very high. In our work, we analyze this effect and show that the Dirichlet log-likelihood criterion classes with low probability induce larger gradients than high-probability classes. This forces the model to focus on the distribution of the ensemble tail-class probabilities. We propose a new training objective that minimizes the reverse KL-divergence to a \emph{Proxy-Dirichlet} target derived from the ensemble. This loss resolves the gradient issues of Ensemble Distribution Distillation, as we demonstrate both theoretically and empirically on the ImageNet and WMT17 En-De datasets containing 1000 and 40,000 classes, respectively.
翻译:机器学习模型的组合能够提高系统性能,并产生可靠和可解释的不确定性估计;然而,它们的推论成本往往高得令人望而却步。 \ emph{ Ensmble 分布蒸馏} 是一种方法,使单一模型能够有效地捕捉一个共同体的预测性能和不确定性估计值。 对于分类,这是通过通过最大可能性标准对组合成员产出分布的分布进行 Dirichlet分布培训而实现的。 虽然在理论上有原则, 但是在对类别数量非常高的大型任务应用时,这一标准显示的趋同性较差。 在我们的工作中,我们分析这一效果并表明,低概率的 Dirichlet 日志类标准类引起比高概率类更大的梯度。 这迫使模型侧重于共性尾级概率的分布。 我们提出了一个新的培训目标,将反向的KL- 调和 emph{Proxy- dirichlet} 目标最小化为集中。 在我们的工作中,我们分析了这一效果, 并显示低概率的 Degleglements 分别含有40, EnalmalMT 和1000 数据。