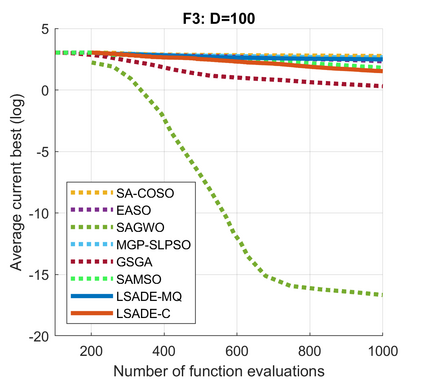
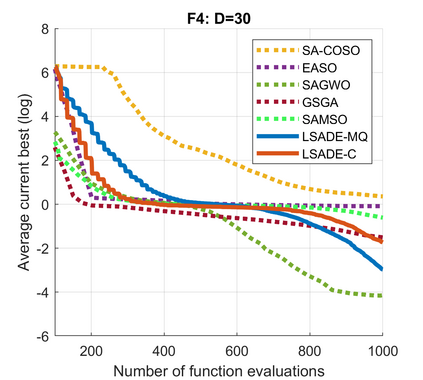
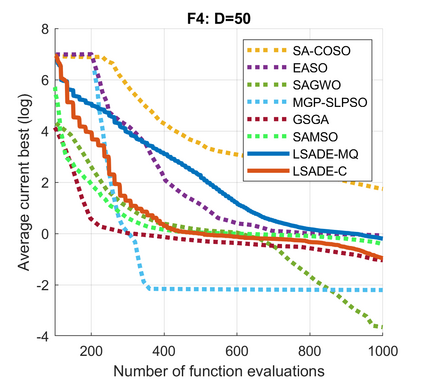
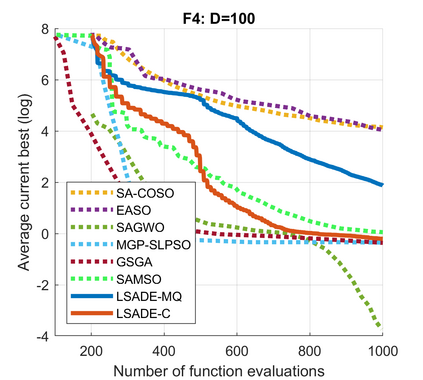
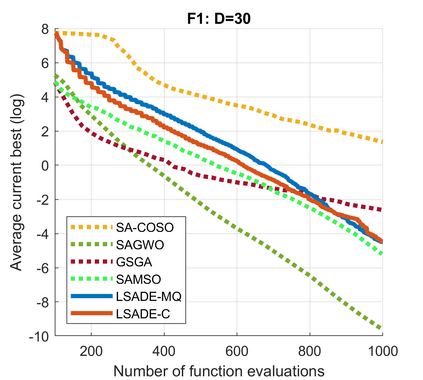
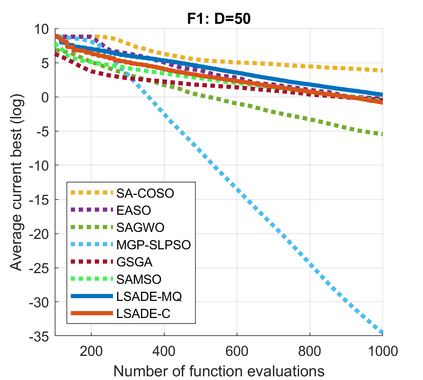
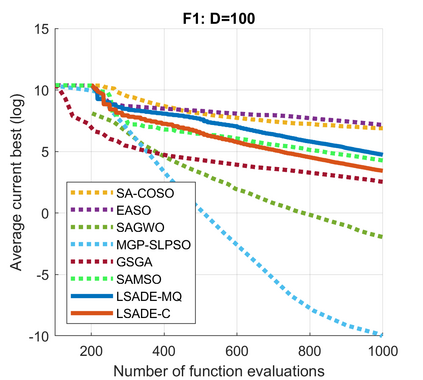
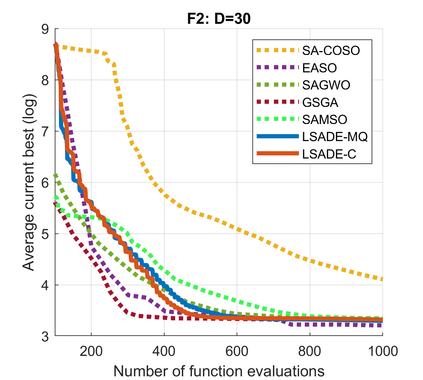
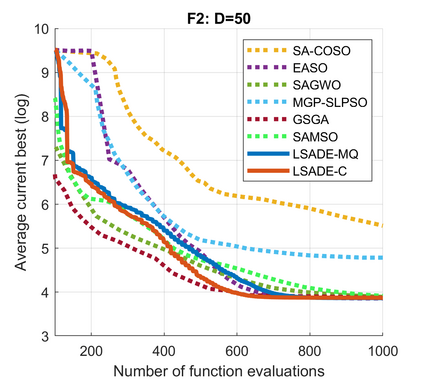
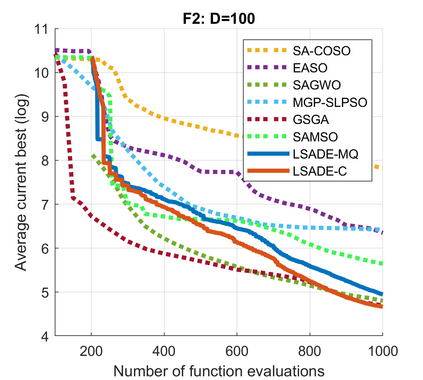
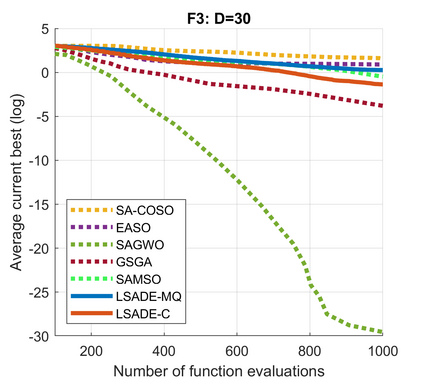
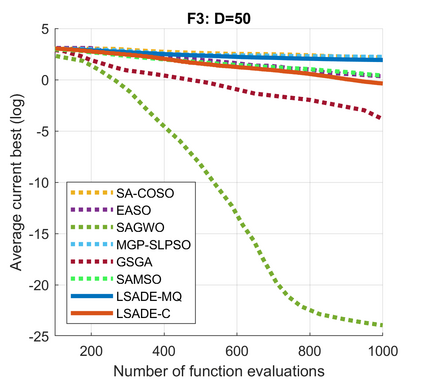
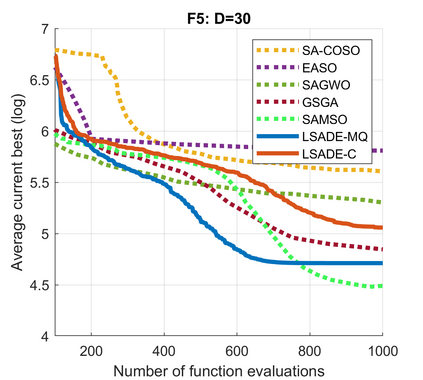
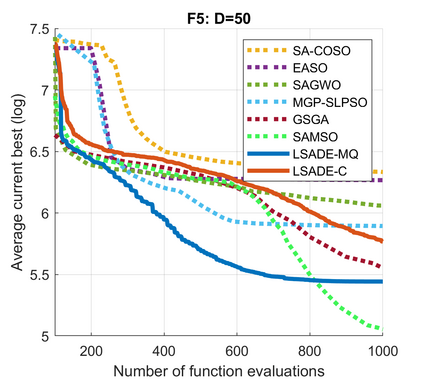
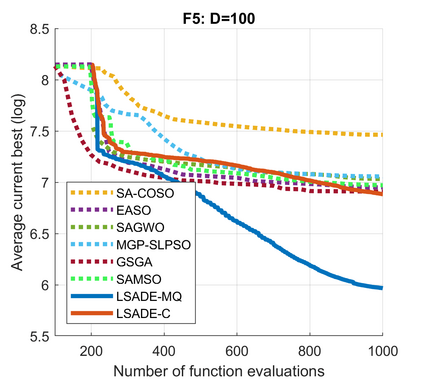
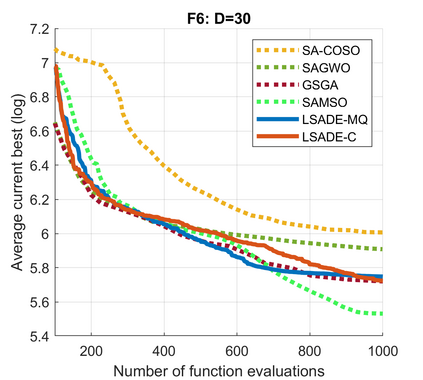
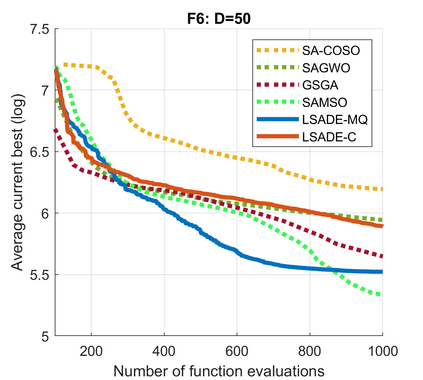
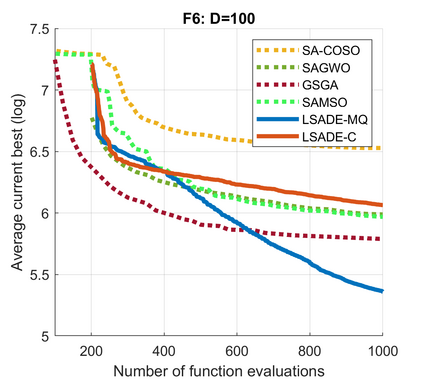
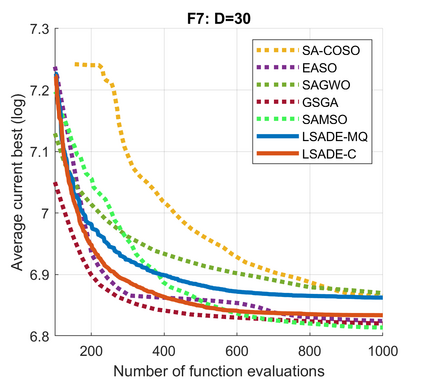
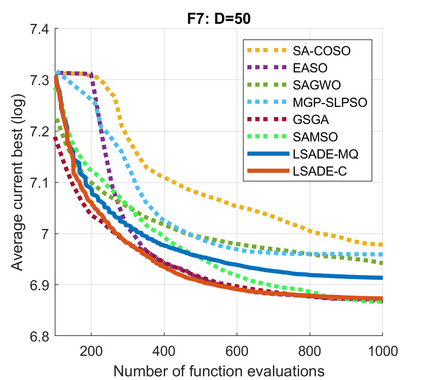
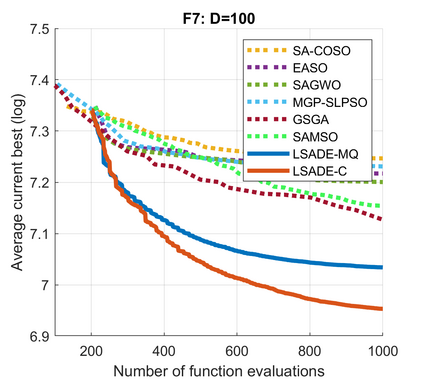
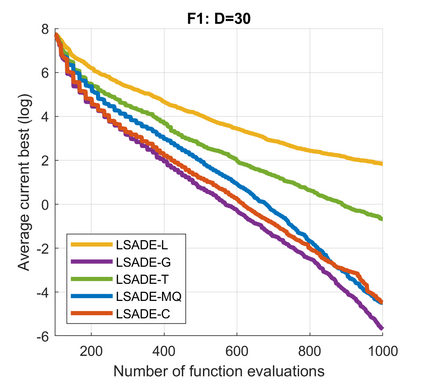
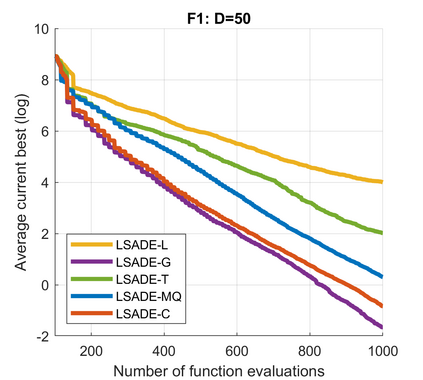
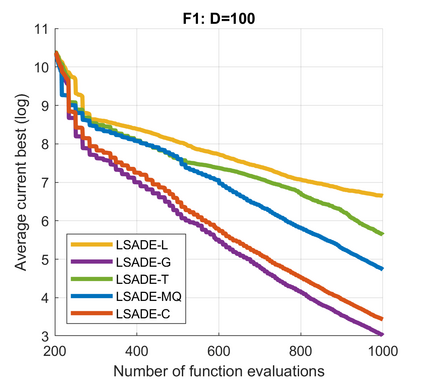
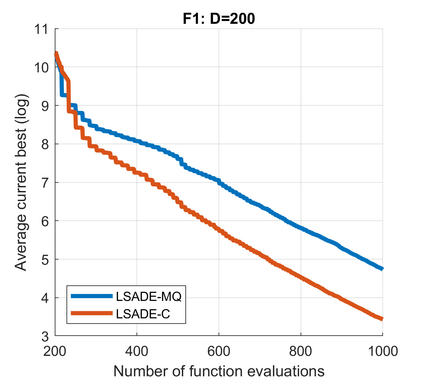
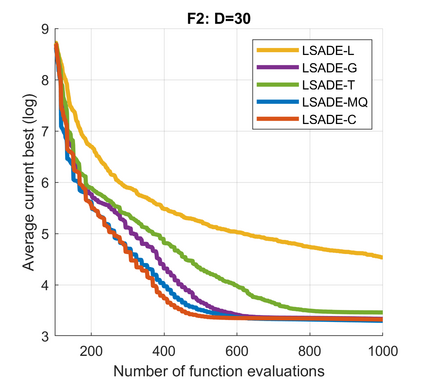
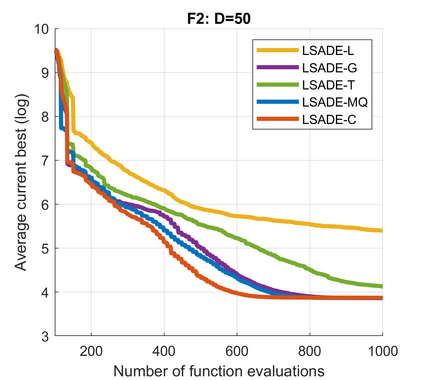
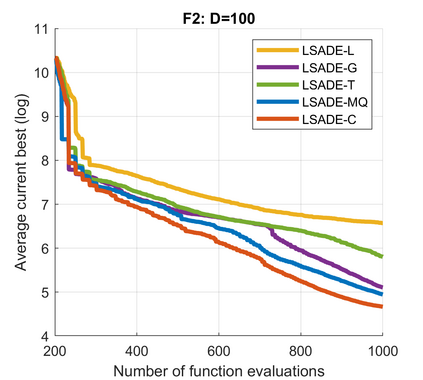
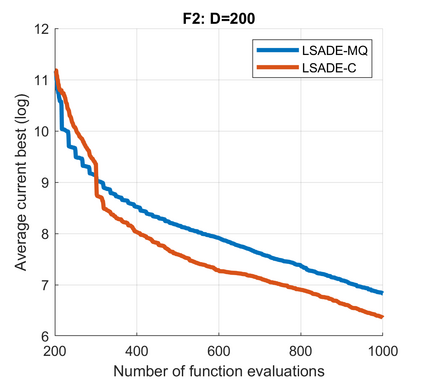
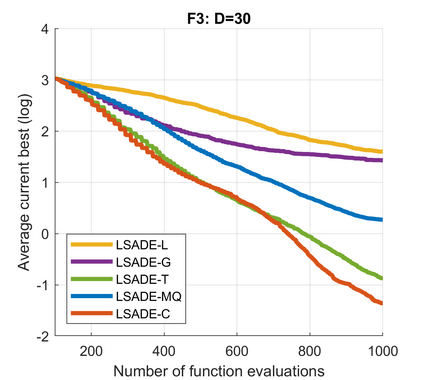
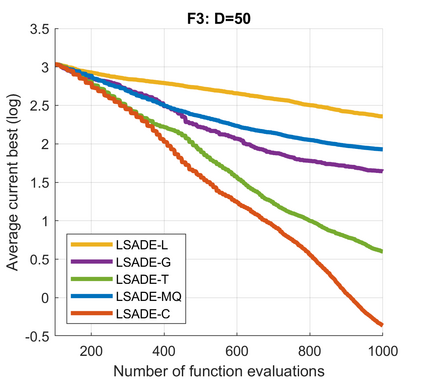
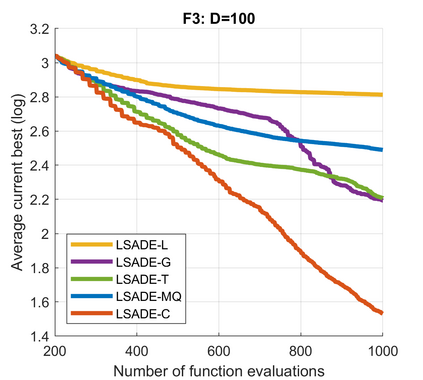
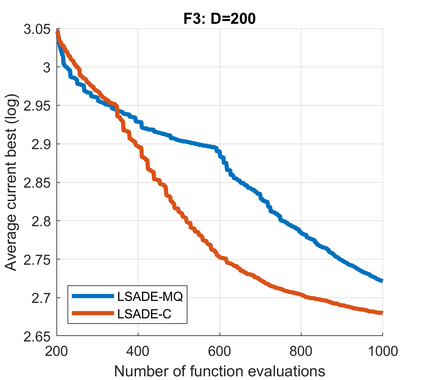
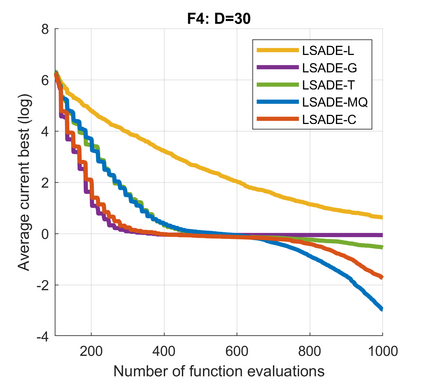
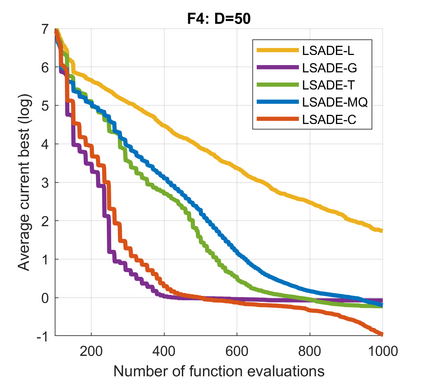
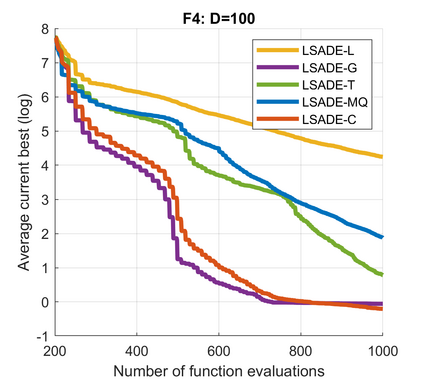
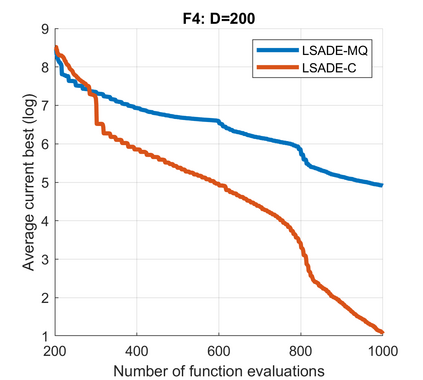
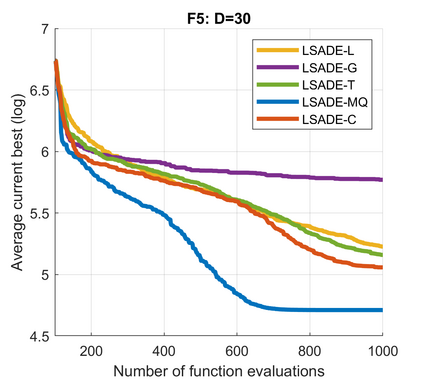
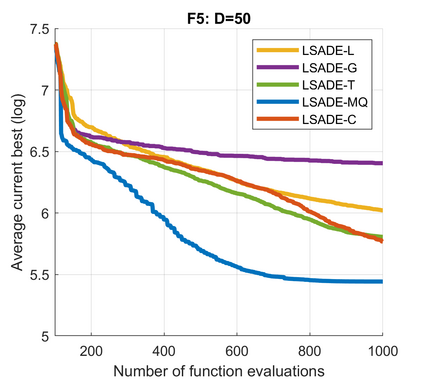
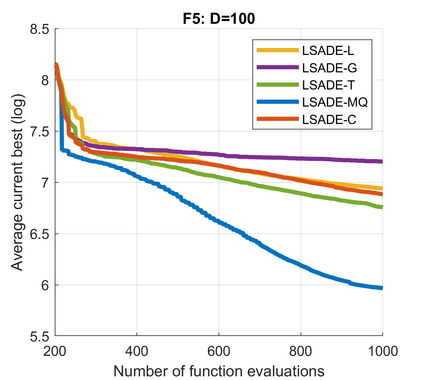
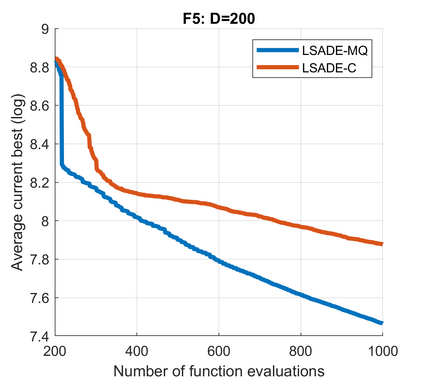
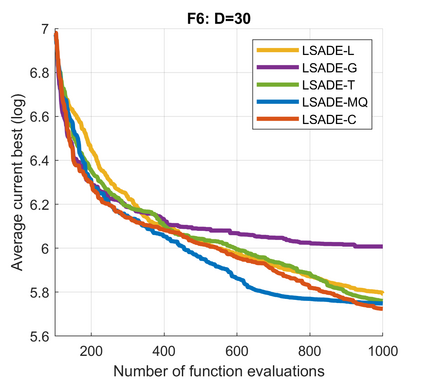
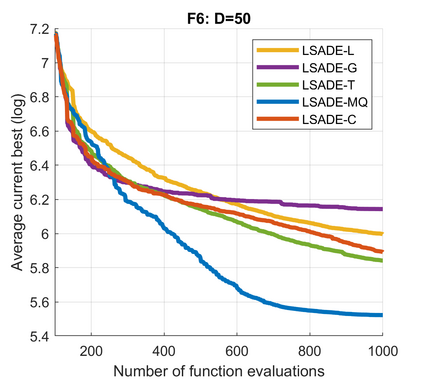
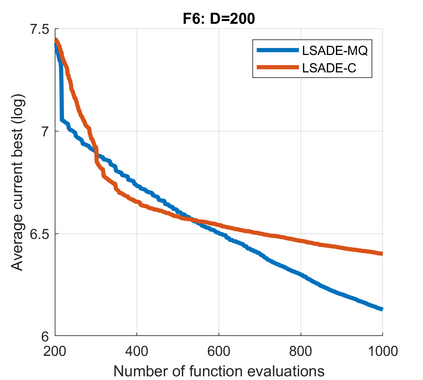
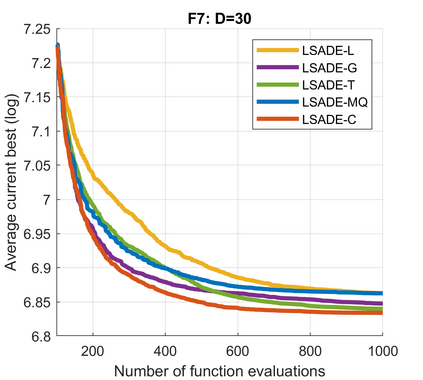
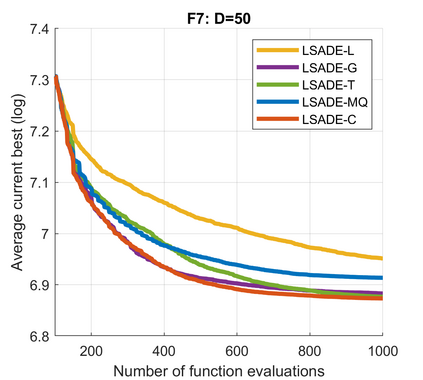
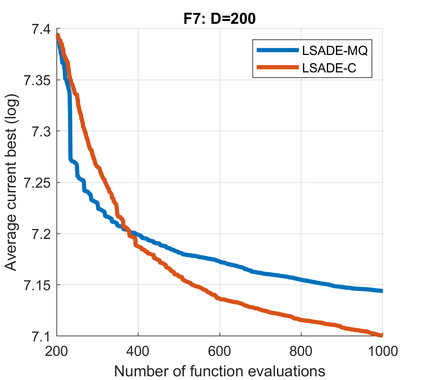
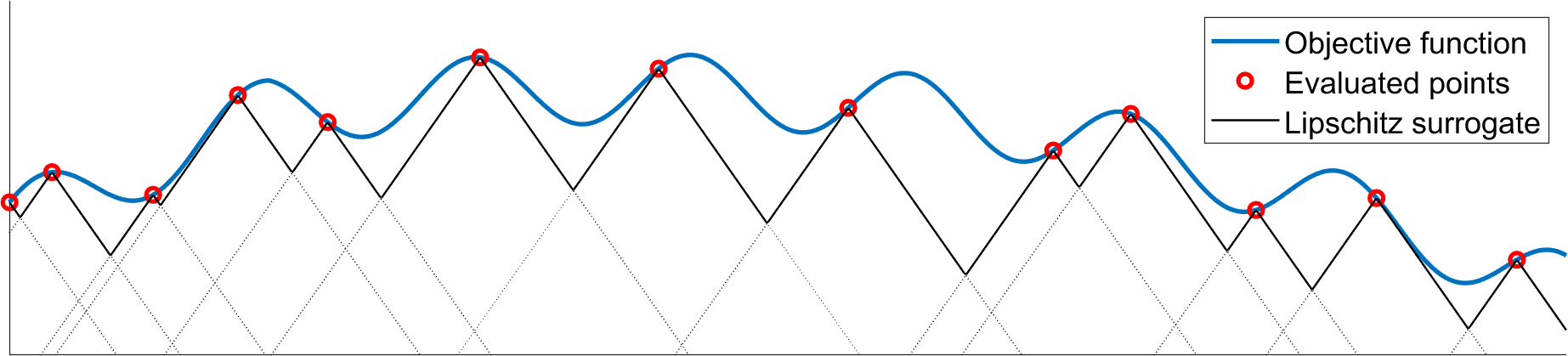
Standard evolutionary optimization algorithms assume that the evaluation of the objective and constraint functions is straightforward and computationally cheap. However, in many real-world optimization problems, the computations of the objective function or constraints involve computationally expensive numerical simulations or physical experiments. Surrogate-assisted evolutionary algorithms (SAEAs) have recently gained increased attention because of their search capabilities for solving these computationally expensive optimization problems. The main idea of SAEAs is the integration of an evolutionary algorithm with a selected surrogate model. In this paper, we propose a novel surrogate model based on a Lipschitz underestimation of the expensive-to-compute objective function. We also develop a differential evolution-based algorithm, that utilizes the Lipschitz-based surrogate model, along with a standard radial basis function surrogate model and a local search procedure. This algorithm, called Lipschitz Surrogate-assisted Differential Evolution (LSADE), is designed for high-dimensional computationally expensive problems. The experimental results on seven benchmark functions of dimensions 30, 50, 100, and 200 show that the proposed method utilizing the Lipschitz-based surrogate model is competitive compared with the state-of-the-art algorithms under a limited computational budget, being especially effective for the very complicated benchmark functions in high dimensions.
翻译:标准进化优化算法假定,对目标和制约功能的评价是简单明了的,而且计算成本低廉。然而,在许多现实世界优化问题中,对目标功能或制约的计算涉及计算费用昂贵的数字模拟或物理实验。超子辅助进化算法(SAEAs)最近因其在解决这些计算昂贵的优化问题的搜索能力而得到越来越多的注意。SAEAs的主要想法是将进化算法与选定的替代模型结合起来。在本文中,我们提议了一个基于利普西茨低估昂贵到可计算目标功能的新替代模型。我们还开发了一种基于不同进化的算法,利用以利普西茨为基础的代进算法模型,同时使用标准的辐射基代进算法模型和本地搜索程序。这个称为利普西茨 Surrogate 辅助差异进化算法(LSADE)的主要想法是为高度计算昂贵的问题设计的。在利普西茨30、50、100和200等七个基准函数的实验结果显示,在基于利普西茨的复杂代进算法下,拟议的方法特别具有竞争力,在高标准级预算下,在高标准级计算中具有竞争性。