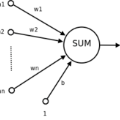
In this article we propose a new deep learning approach to approximate operators related to parametric partial differential equations (PDEs). In particular, we introduce a new strategy to design specific artificial neural network (ANN) architectures in conjunction with specific ANN initialization schemes which are tailor-made for the particular approximation problem under consideration. In the proposed approach we combine efficient classical numerical approximation techniques with deep operator learning methodologies. Specifically, we introduce customized adaptions of existing ANN architectures together with specialized initializations for these ANN architectures so that at initialization we have that the ANNs closely mimic a chosen efficient classical numerical algorithm for the considered approximation problem. The obtained ANN architectures and their initialization schemes are thus strongly inspired by numerical algorithms as well as by popular deep learning methodologies from the literature and in that sense we refer to the introduced ANNs in conjunction with their tailor-made initialization schemes as Algorithmically Designed Artificial Neural Networks (ADANNs). We numerically test the proposed ADANN methodology in the case of several parametric PDEs. In the tested numerical examples the ADANN methodology significantly outperforms existing traditional approximation algorithms as well as existing deep operator learning methodologies from the literature.
翻译:暂无翻译