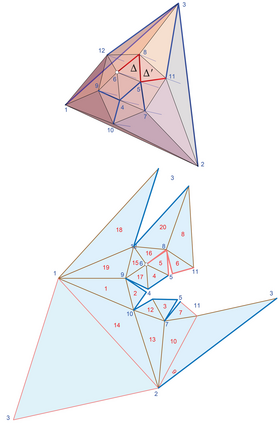
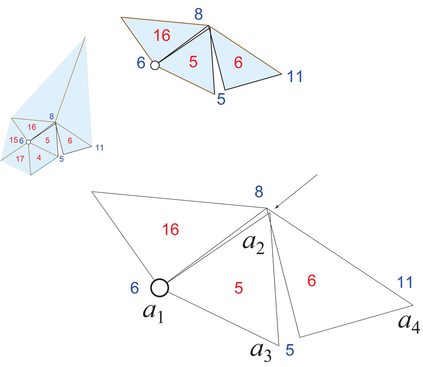
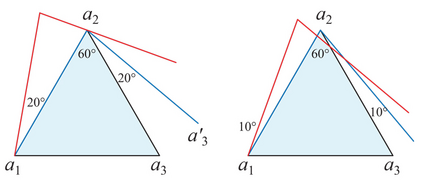
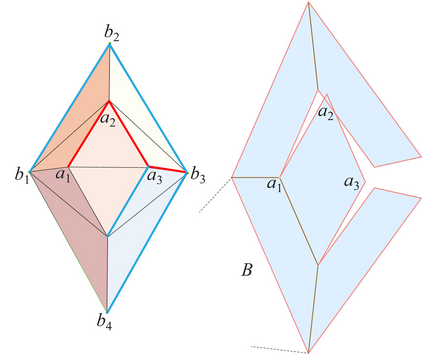
Ghomi proved that every convex polyhedron could be stretched via an affine transformation so that it has an edge-unfolding to a net [Gho14]. A net is a simple planar polygon; in particular, it does not self-overlap. One can view his result as establishing that every combinatorial polyhedron has a metric realization that allows unfolding to a net. Joseph Malkevitch asked if the reverse holds (in some sense of ``reverse"): Is there a combinatorial polyhedron such that, for every metric realization P in R^3, and for every spanning cut-tree T, P cut by T unfolds to a net? In this note we prove the answer is NO: every combinatorial polyhedron has a realization and a cut-tree that unfolds the polyhedron with overlap.
翻译:Ghomi证明,每一个锥形多元面都可以通过仙形变形而伸展,这样它就能从边缘翻到一个网[Gho14]。网是一个简单的平面多边形;特别是,它不会自我重叠。我们可以通过确定每个组合式多元面都有一个允许向网展示的量化认识来查看他的结果。Joseph Malkevitch问反向是否持有(某种“反向”感知 ):是否有组合式多元面,对于R3中的每一项指标实现P,以及对于每一个横跨切开的T树,P被T切到一个网?在本说明中,我们证明答案是NO:每个组合式多元面都有一个实现和切开的多面带重叠的圆形树。