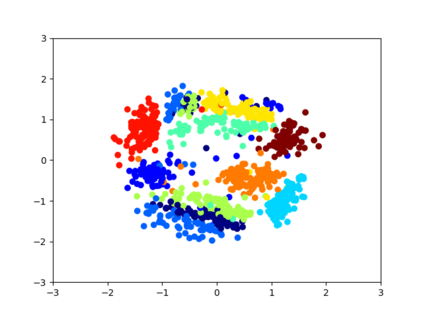
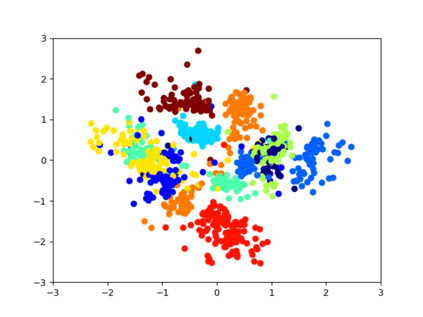
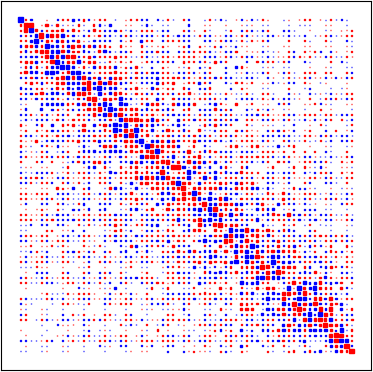
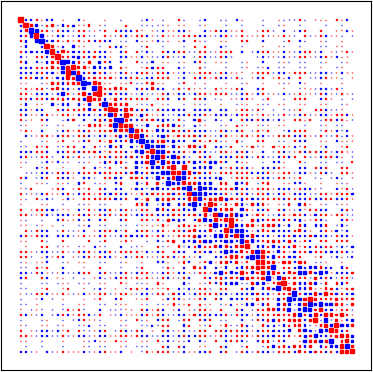
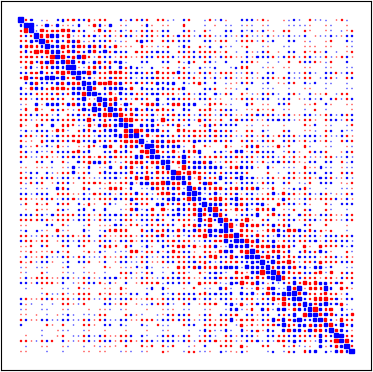
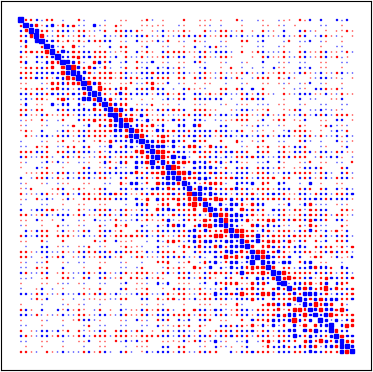
Several regularization methods have recently been introduced which force the latent activations of an autoencoder or deep neural network to conform to either a Gaussian or hyperspherical distribution, or to minimize the implicit rank of the distribution in latent space. In the present work, we introduce a novel regularizing loss function which simulates a pairwise repulsive force between items and an attractive force of each item toward the origin. We show that minimizing this loss function in isolation achieves a hyperspherical distribution. Moreover, when used as a regularizing term, the scaling factor can be adjusted to allow greater flexibility and tolerance of eccentricity, thus allowing the latent variables to be stratified according to their relative importance, while still promoting diversity. We apply this method of Eccentric Regularization to an autoencoder, and demonstrate its effectiveness in image generation, representation learning and downstream classification tasks.
翻译:最近采用了几种正规化方法,迫使自动编码器或深神经网络的潜在启动符合高斯分布或超球分布,或最大限度地降低潜空空间分布的隐性等级。在目前的工作中,我们引入了一种新的常规化损失功能,在物品之间模拟一种双向反作用,对每个物品的吸引力力量对源头进行模拟。我们表明,孤立地将这一损失功能最小化可以实现超球分布。此外,在作为常规化术语使用时,可调整缩放系数,以允许更大的灵活性和对偏心度的容忍度,从而使潜在变量根据其相对重要性进行分层,同时仍然促进多样性。我们将这种中心化方法应用于自动编码器,并展示其在图像生成、代言式学习和下游分类任务方面的效力。