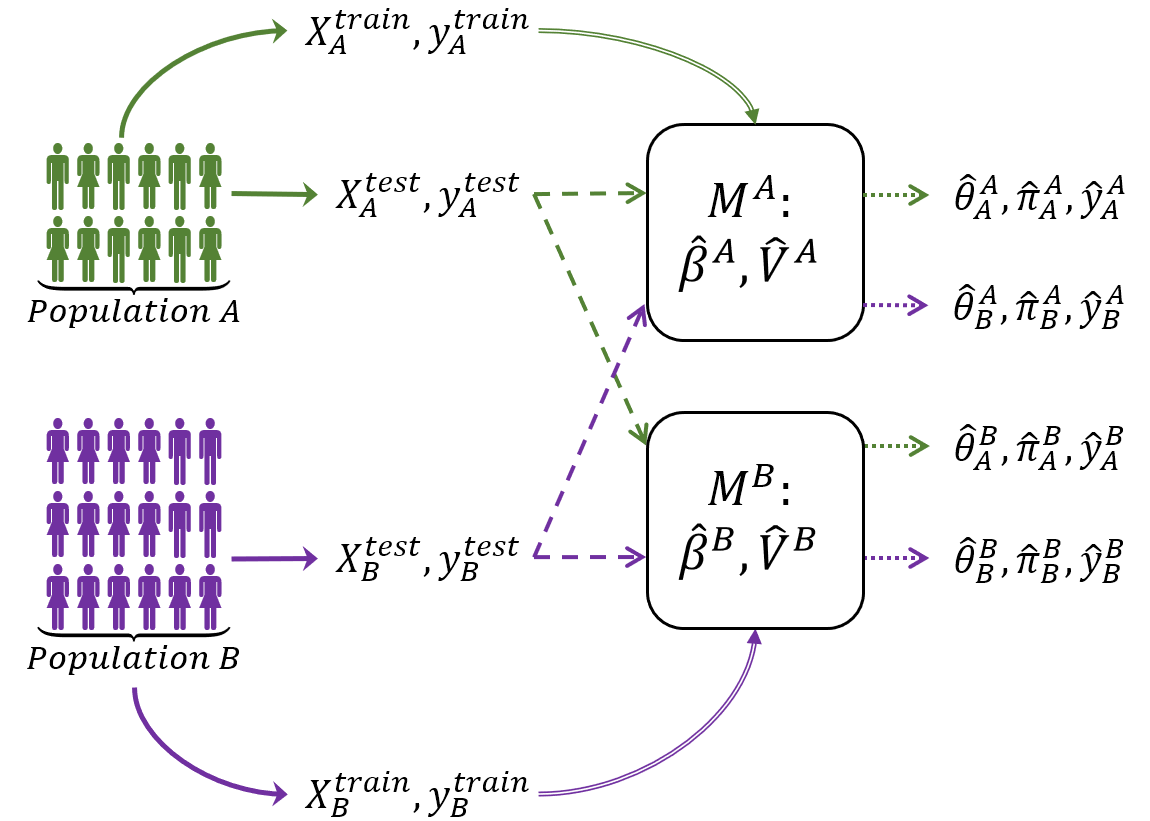
In this paper we discuss how to evaluate the differences between fitted logistic regression models across sub-populations. Our motivating example is in studying computerized diagnosis for learning disabilities, where sub-populations based on gender may or may not require separate models. In this context, significance tests for hypotheses of no difference between populations may provide perverse incentives, as larger variances and smaller samples increase the probability of not-rejecting the null. We argue that equivalence testing for a prespecified tolerance level on population differences incentivizes accuracy in the inference. We develop a cascading set of equivalence tests, in which each test addresses a different aspect of the model: the way the phenomenon is coded in the regression coefficients, the individual predictions in the per example log odds ratio and the overall accuracy in the mean square prediction error. For each equivalence test, we propose a strategy for setting the equivalence thresholds. The large-sample approximations are validated using simulations. For diagnosis data, we show examples for equivalent and non-equivalent models.
翻译:本文讨论如何评估拟合的Logistic回归模型在不同子群体间的差异。我们的案例是研究学习障碍的计算机自动诊断,其中基于性别的不同子群体可能需要不同的模型。在这种情况下,检验零假设差异不存在可能会产生错误激励,因为参数的方差变大或样本量变小都会导致不拒绝零假设。我们认为,基于预先规定的容忍度等价测试方法对群体差异进行推断更为准确。我们开发了一系列级联等价测试,每个测试都涉及模型的不同方面:现象在回归系数中的编码方式,单个样本的对数几率比中的个体预测,以及平均平方预测误差中的整体准确性。对于每个等价测试,我们提出了一种设置等价阈值的策略。使用模拟验证了大样本近似。对于诊断数据,我们展示了等价和不等价模型的示例。