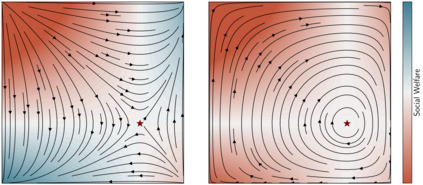
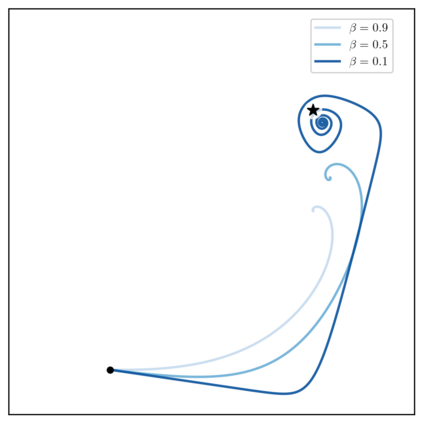
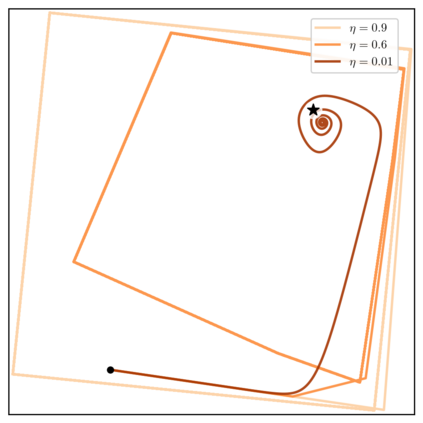
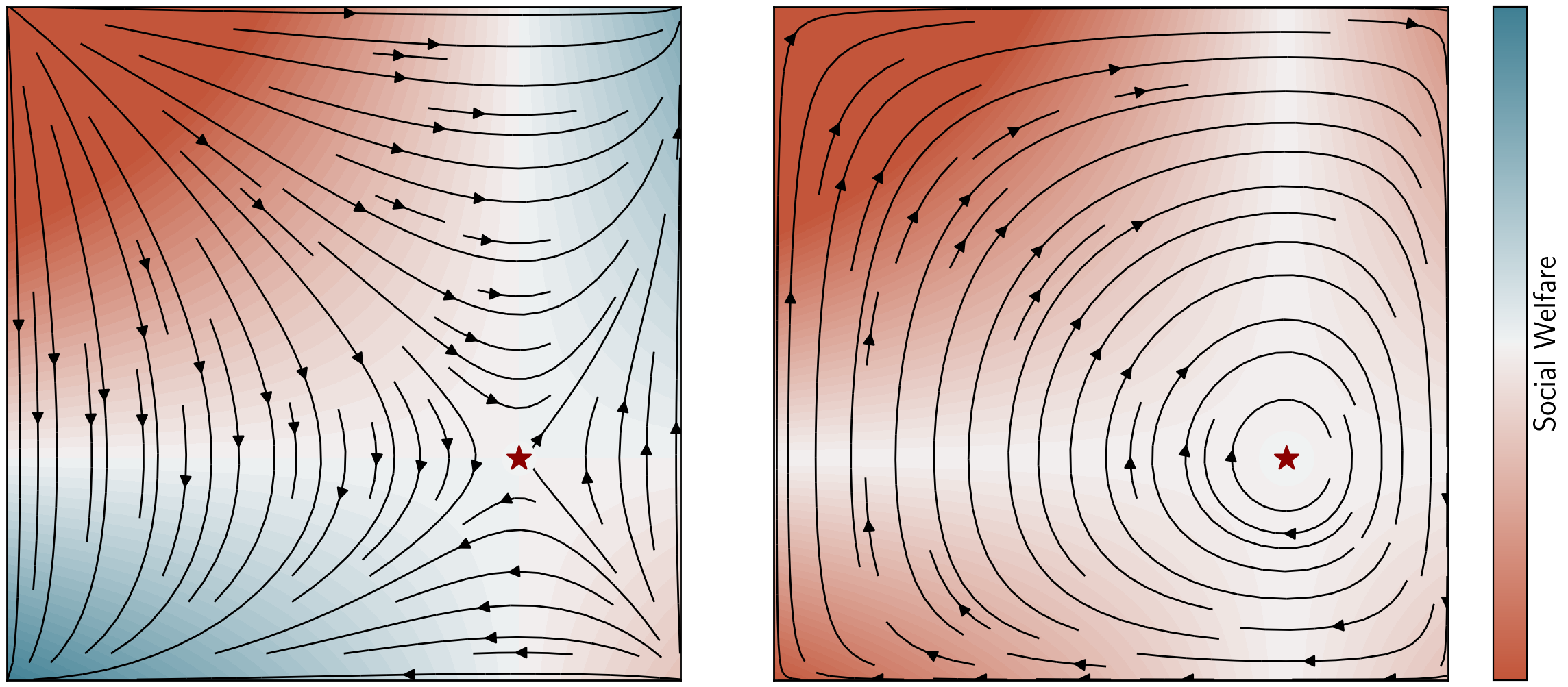
We extend the study of learning in games to dynamics that exhibit non-asymptotic stability. We do so through the notion of uniform stability, which is concerned with equilibria of individually utility-seeking dynamics. Perhaps surprisingly, it turns out to be closely connected to economic properties of collective rationality. Under mild non-degeneracy conditions and up to strategic equivalence, if a mixed equilibrium is not uniformly stable, then it is not weakly Pareto optimal: there is a way for all players to improve by jointly deviating from the equilibrium. On the other hand, if it is locally uniformly stable, then the equilibrium must be weakly Pareto optimal. Moreover, we show that uniform stability determines the last-iterate convergence behavior for the family of incremental smoothed best-response dynamics, used to model individual and corporate behaviors in the markets. Unlike dynamics around strict equilibria, which can stabilize to socially-inefficient solutions, individually utility-seeking behaviors near mixed Nash equilibria lead to collective rationality.
翻译:暂无翻译