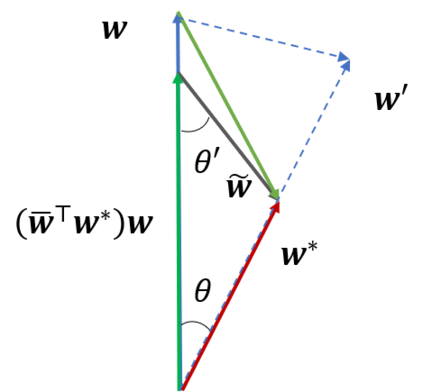
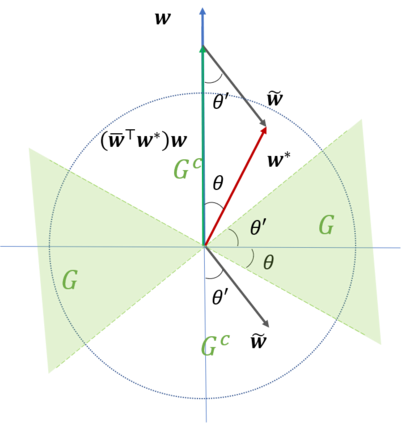
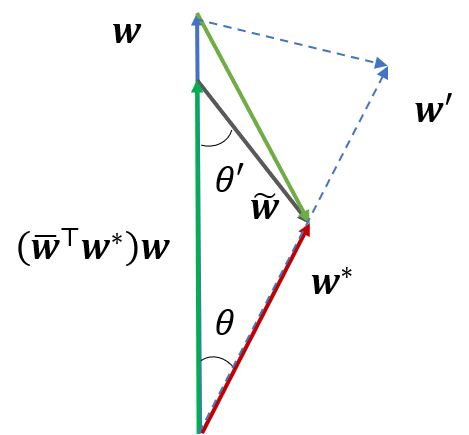
We analyze the properties of adversarial training for learning adversarially robust halfspaces in the presence of agnostic label noise. Denoting $\mathsf{OPT}_{p,r}$ as the best robust classification error achieved by a halfspace that is robust to perturbations of $\ell_{p}$ balls of radius $r$, we show that adversarial training on the standard binary cross-entropy loss yields adversarially robust halfspaces up to (robust) classification error $\tilde O(\sqrt{\mathsf{OPT}_{2,r}})$ for $p=2$, and $\tilde O(d^{1/4} \sqrt{\mathsf{OPT}_{\infty, r}} + d^{1/2} \mathsf{OPT}_{\infty,r})$ when $p=\infty$. Our results hold for distributions satisfying anti-concentration properties enjoyed by log-concave isotropic distributions among others. We additionally show that if one instead uses a nonconvex sigmoidal loss, adversarial training yields halfspaces with an improved robust classification error of $O(\mathsf{OPT}_{2,r})$ for $p=2$, and $O(d^{1/4}\mathsf{OPT}_{\infty, r})$ when $p=\infty$. To the best of our knowledge, this is the first work to show that adversarial training provably yields robust classifiers in the presence of noise.
翻译:我们分析用于学习对抗性强的半空的对抗性培训的特性, 以备在标签噪声中学习对抗性强的半空 。 将 $\ mathsf{ OPT} p}, r} 美元作为半空中最可靠的分类错误 。 半空中对扰动 $\ ell ⁇ p} 美元 半球 美元 美元 半半空 方圆 美元, 我们显示, 标准二进制交叉性损失的对抗性培训, 以 $ (robty) 分类错误 $ (robty), O(sqr) $ 2, 美元 美元, 美元 美元, 美元 美元, 美元, 美元 美元, 美元 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 对抗性半调的半的半位 。