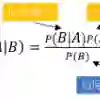
Due to its linear complexity, naive Bayes classification remains an attractive supervised learning method, especially in very large-scale settings. We propose a sparse version of naive Bayes, which can be used for feature selection. This leads to a combinatorial maximum-likelihood problem, for which we provide an exact solution in the case of binary data, or a bound in the multinomial case. We prove that our convex relaxation bounds becomes tight as the marginal contribution of additional features decreases, using a priori duality gap bounds dervied from the Shapley-Folkman theorem. We show how to produce primal solutions satisfying these bounds. Both binary and multinomial sparse models are solvable in time almost linear in problem size, representing a very small extra relative cost compared to the classical naive Bayes. Numerical experiments on text data show that the naive Bayes feature selection method is as statistically effective as state-of-the-art feature selection methods such as recursive feature elimination, $l_1$-penalized logistic regression and LASSO, while being orders of magnitude faster.
翻译:暂无翻译