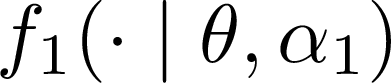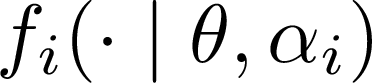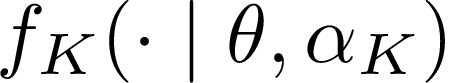Consider $K$ processes, each generating a sequence of identical and independent random variables. The probability measures of these processes have random parameters that must be estimated. Specifically, they share a parameter $\theta$ common to all probability measures. Additionally, each process $i\in\{1, \dots, K\}$ has a private parameter $\alpha_i$. The objective is to design an active sampling algorithm for sequentially estimating these parameters in order to form reliable estimates for all shared and private parameters with the fewest number of samples. This sampling algorithm has three key components: (i)~data-driven sampling decisions, which dynamically over time specifies which of the $K$ processes should be selected for sampling; (ii)~stopping time for the process, which specifies when the accumulated data is sufficient to form reliable estimates and terminate the sampling process; and (iii)~estimators for all shared and private parameters. Owing to the sequential estimation being known to be analytically intractable, this paper adopts \emph {conditional} estimation cost functions, leading to a sequential estimation approach that was recently shown to render tractable analysis. Asymptotically optimal decision rules (sampling, stopping, and estimation) are delineated, and numerical experiments are provided to compare the efficacy and quality of the proposed procedure with those of the relevant approaches.
翻译:考虑 $K 进程, 每个过程产生一个相同和独立的随机变量序列。 这些过程的概率度量有随机参数, 并且必须估算。 具体地说, 这些过程的概率度量有随机参数。 具体地说, 它们共有一个参数 $\ theta$, 所有概率度量都是共同的。 此外, 每个过程 $\\%1,\ dots, K ⁇ $ 美元有一个私人参数 $alpha_ i 美元。 目标是设计一个主动的抽样算法, 用于按顺序估计这些参数, 以便对所有共享和私人参数得出可靠的估计, 并使用数量最少的样本。 这个抽样算法有三个关键组成部分:(一) ~ 由数据驱动的抽样决定, 并动态地指出应该选择美元过程的哪个过程进行取样;(二) 停止过程的时间, 规定累积的数据何时足以形成可靠的估计并终止取样过程; 和 (三) 所有共享和私人参数的测算器, 目的是根据已知的测序进行可靠的估计, 本文采用了成本估算功能, 导致一种连续的估算方法, 最近显示的测算方法, 使分析具有可测量性, 和最佳的测算。