Independence testing in high dimensions

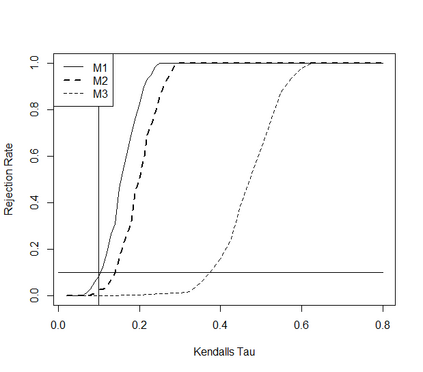
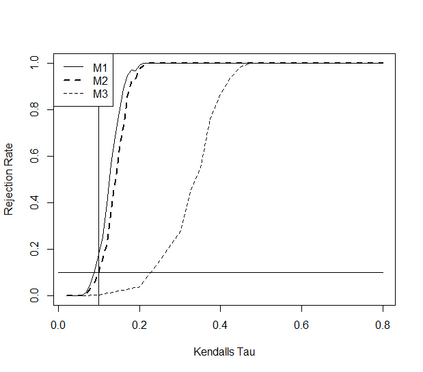
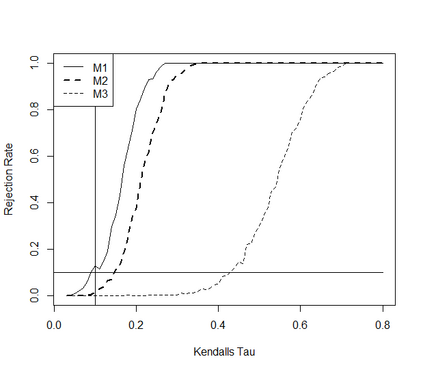
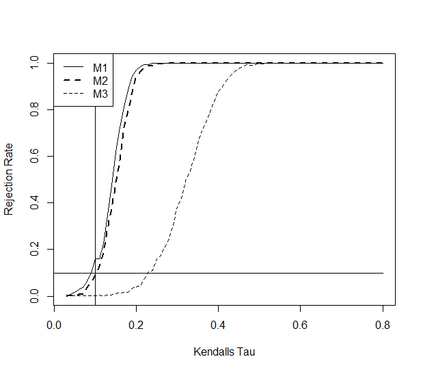
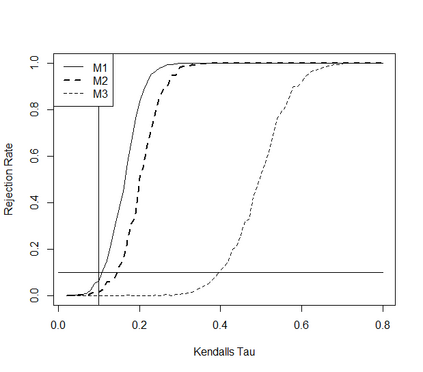
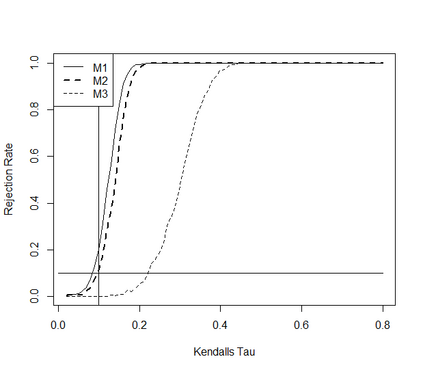
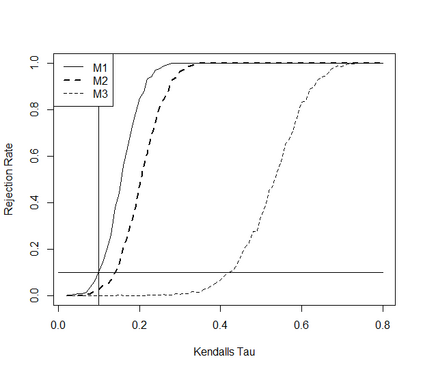
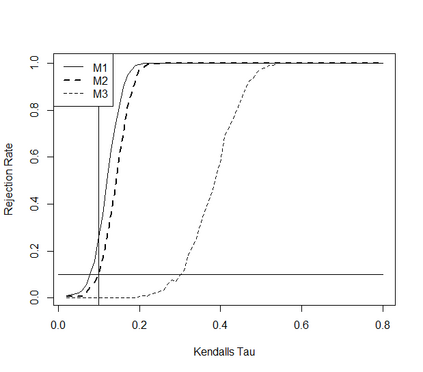
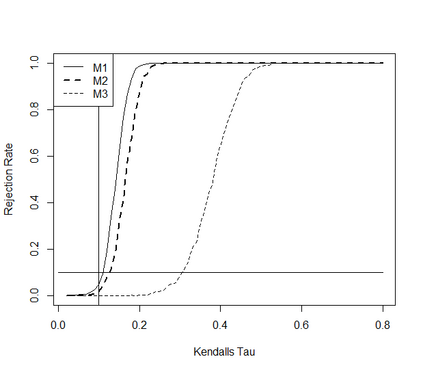
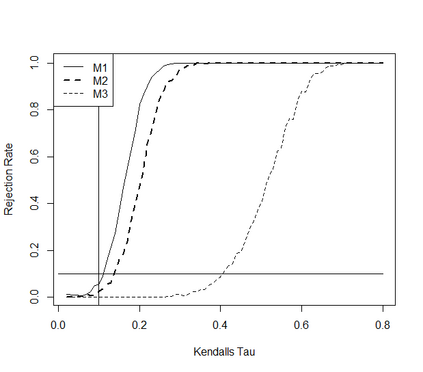
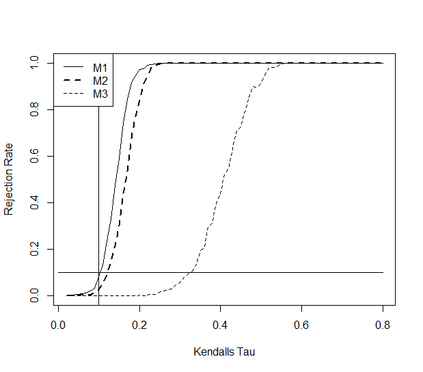
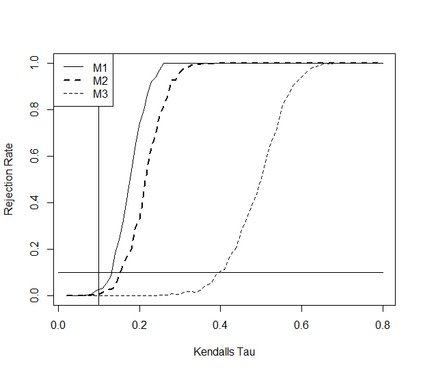
This paper takes a different look on the problem of testing the mutual independence of the components of a high-dimensional vector. Instead of testing if all pairwise associations (e.g. all pairwise Kendall's $\tau$) between the components vanish, we are interested in the (null)-hypothesis that all pairwise associations do not exceed a certain threshold in absolute value. The consideration of these hypotheses is motivated by the observation that in the high-dimensional regime, it is rare, and perhaps impossible, to have a null hypothesis that can be exactly modeled by assuming that all pairwise associations are precisely equal to zero. The formulation of the null hypothesis as a composite hypothesis makes the problem of constructing tests non-standard and in this paper we provide a solution for a broad class of dependence measures, which can be estimated by $U$-statistics. In particular we develop an asymptotic and a bootstrap level $\alpha$-test for the new hypotheses in the high-dimensional regime. We also prove that the new tests are minimax-optimal and demonstrate good finite sample properties by means of a small simulation study.